Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 13

Расстояния между   и точными значениями  (i = 0, 1, 2,…, n) вычислим по приближенным формулам

 (для метода Эйлера),                                       (13)

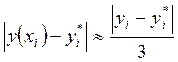 (для обеих модификаций метода Эйлера).  (14)

Пример.

Пусть численное решение дифференциального уравнения  ищется при помощи метода Эйлера с шагом h = 0,2. Требуется найти  и , соответствующие аргументу  = 1,2, и оценить погрешность .

При h = 0,2 получим

 = 1 + 0,2ּ2 = 1,4.

Теперь проведем двукратные вычисления с шагом  = 0,1. Сначала находим = 1,1 и

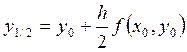 = 1 + 0,1ּ2 = 1,2.

Затем вычисляем значение :

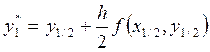 = 1,2 + 0,1ּ2,65 = 1,465.

С помощью (13) найдем приблизительную оценку погрешности

= 0,065.

Метод Рунге – Кутта

Метод Рунге-Кутта является одним из наиболее употребительных методов повышенной точности.

Пусть дано дифференциальное уравнение

                                                                               (14)

с начальным условием . Нужно найти решение уравнения (14) на отрезке [a, b].

Выбираем малый шаг h и на отрезке [a, b] строим систему равноотстоящих точек

,  (i = 0, 1, 2,…, n).

Наиболее распространенным на практике является метод Рунге – Кутта четвертого порядка точности. Для перехода от точки  к  требуется вычислить четыре числа:

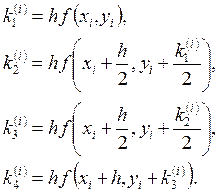                                                                   (15)

Тогда последовательные значения  искомой функции определяются по формуле

,

где

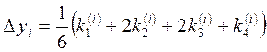 (i = 0, 1, 2,…, n).                                                 (16)

Метод Рунге-Кутта также можно применять для нахождения решения  дифференциальных уравнений более высокого порядка и для систем уравнений.

Пусть дана система дифференциальных уравнений

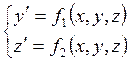,                                                                        (17)

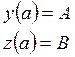, на интервале [a, b].

Разобьем интервал на n точек, шаг разбиения .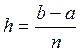

Итерационные формулы метода Рунге-Кутта для данной системы будут иметь следующий вид:

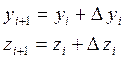,                                                                         (18)

где

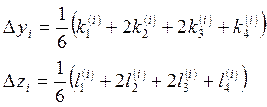 (i = 0, 1, 2,…, n).

Соответствующие числа  и  (j = 1, 2, 3, 4) вычисляются следующим образом

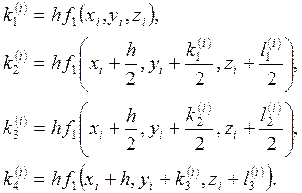
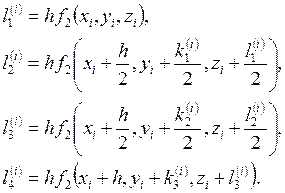                                                                                 (19)

Прежде, чем применять метод Рунге-Кутта для решения дифференциальных уравнений более высоких порядков, необходимо понизить порядок уравнения (до первого порядка). В результате этого уравнение преобразуется в систему уравнений первого порядка и уже непосредственно к системе применяется метод Рунге-Кутта.

Пример.

Методом Рунге-Кутта решить дифференциальное уравнение

, , на интервале [0; 0,5].

Формула метода Рунге-Кутта имеет вид =,

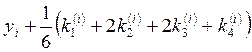где

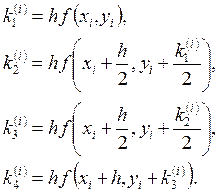(i = 0, 1, 2,…, n).                                                  

Интервал [0; 0,5] разделим на n = 5 точек, шаг разбиения .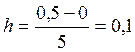

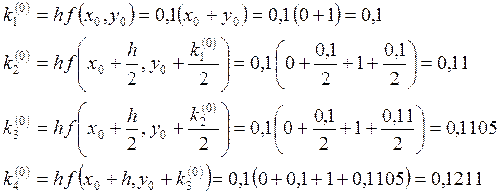
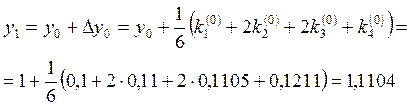
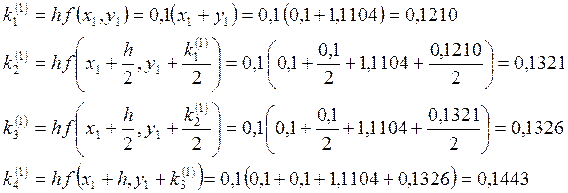
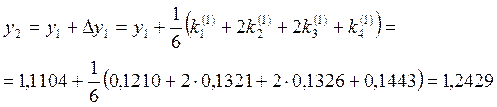
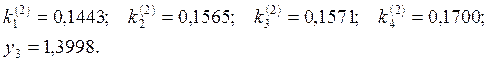
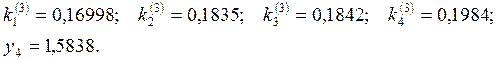
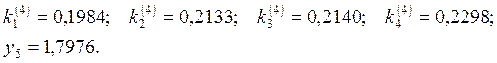
В результате получили таблицу значений , (i = 0, 1, 2, 3, 4, 5).

Метод Рунге-Кутта позволяет находить решения дифференциальных уравнений, используя переменный шаг.

Рассмотрим использование метода Рунге-Кутта с переменным шагом для рассмотренного выше уравнения.

Значения  находим, используя шаг .

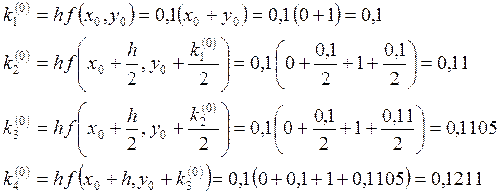
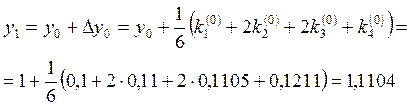
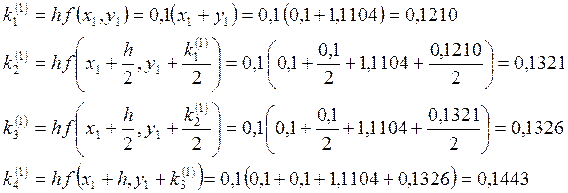
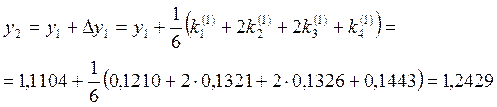
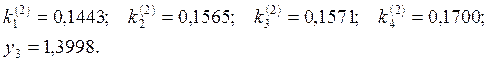
Далее меняем шаг и положим .

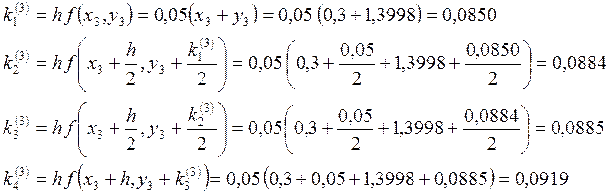
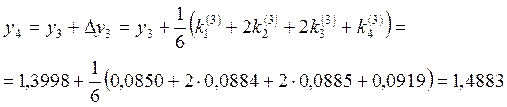
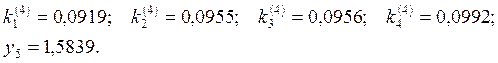
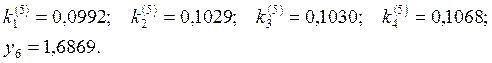
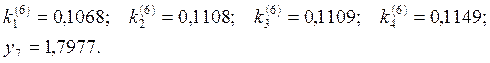
Метод сеток (конечных разностей) решения краевой задачи для обыкновенного дифференциального уравнения

Для решения краевых задач может быть использован метод конечных разностей, заключающийся в замене дифференциальных операторов разностными операторами.

Рассмотрим на отрезке [a, b] граничную задачу для дифференциального уравнения

                                                                   (20)

с условиями

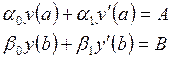,                                                                         (21)

где p(x), q(x), f(x) непрерывны на отрезке [a, b].

Метод сеток для решения граничной задачи состоит в следующем. Область задания дифференциального уравнения (в данном случае – отрезок [a, b]) заменяется некоторой дискретной (сеточной) областью. Для этого разобьем отрезок [a, b] на n равных частей точками

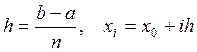, (i = 0, 1, 2,…, n).                                         (22)

Точки  называются узлами сетки. Совокупность этих точек называется сеткой. В каждом из узлов  сетки заменим производную, входящую в уравнение (20), конечно-разностными соотношениями. Получим систему  уравнений относительно . Если в граничные условия входят производные (как в условиях (21)), то их тоже заменяем соответствующими конечно-разностными соотношениями.