Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 10

3.4. Вывести формулу для приближенного извлечения корней  (1 ≤ x ≤ 100), используя значения x₀ = 1, y₀ = 1, x₁ = 25, y₁ = 5, x₂ = 100, y₂ = 10.

3.5. Вывести приближенную формулу вида  (0 ≤ x ≤ 90), используя значения 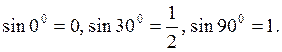 Пользуясь этой формулой, приближенно найти: .

3.6. Построить для функции  на сегменте [-1,1] интерполяционный многочлен Лагранжа, приняв за узлы точки: x = 0, ±, ±1.

3.7. Оценить погрешность приближения функции  интерполяционным полиномом Лагранжа , построенном по узлам  в точке: 1) x = 0,05;  2) x = 0,15.

3.8. Функция  приближается на отрезке 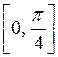 интерполяционным полиномом по значениям в точках 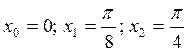. Оценить погрешность интерполяции на этом отрезке.

3.9. Оценить погрешность интерполяции функции  на отрезке [0;1] интерполяционным полиномом Лагранжа , построенном на равномерной сетке.

3.10. Оценить число узлов интерполяции на отрезке 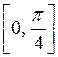, обеспечивающее точность

ε ≤ 10^-2 точность приближения функции .

3.11. С каким шагом следует составлять таблицу функции  на 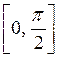, чтобы погрешность линейной интерполяции не превосходила 0,5ּ10^-6 ?

3.12. Определить степень полинома Лагранжа на равномерной сетке, обеспечивающую точность приближения функции  на [0;1] не хуже 10^-3.

3.13. Пусть функция  задана на отрезке . При каком b полином Лагранжа , построенный на равномерной сетке, приближает эту функцию с погрешностью ε ≤ 10^-3 ?

3.14. Построить интерполяционный тригонометрический полином второй степени , удовлетворяющий условиям: .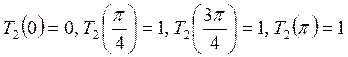

3.15. Построить интерполяционный тригонометрический полином минимальной степени по заданным значениям .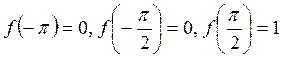

3.16. Построить многочлен , удовлетворяющий условиям .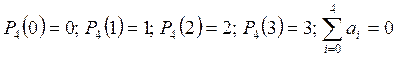

3.17. Построить полином Лагранжа  степени (n-1), удовлетворяющий условиям .

1)

2) .

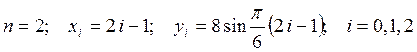3.18. Функцию  на интервале [-1;1] квадратично аппроксимировать полиномом третьей степени вида 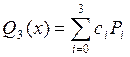, где  - полиномы Лежандра.

3.19. Функция задана таблицей

Построить для y = f(x) аппроксимирующий полином второй степени .

3.20. Функцию на интервале  аппроксимировать тригонометрическим полиномом .

3.21. Построить аппроксимирующий полином второй степени для функции, заданной таблицей

4. Численное интегрирование

Формула Ньютона – Котеса:

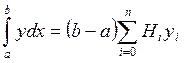,                                                                         (1)

где 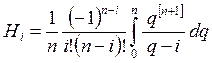 (i = 0, 1, 2,…, n) – коэффициенты Ньютона – Котеса,

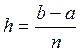 - шаг разбиения интервала [a, b] на n точек.

Для коэффициентов Ньютона – Котеса справедливы следующие соотношения:

1) ;

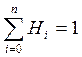2) .