Решение алгебраических и трансцендентных уравнений. Метод сеток решения уравнений параболического типа, страница 11

Недостатком метода Ньютона-Котеса является то, что при больших n в формуле (1) будут встречаться как положительные, так и отрицательные коэффициенты , превосходящие по абсолютной величине достаточно большое число. При больших n могут появиться большие погрешности при вычислении интегралов. Поэтому формулы Ньютона-Котеса малопригодны для вычислений, когда число узлов n будет большим.

Пример.

Вычислить интеграл 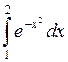 методом Ньютона-Котеса.

Интервал [1, 2] разобьем на n = 5 точек, шаг разбиения .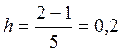

Тогда, согласно формуле (1), будем иметь

.

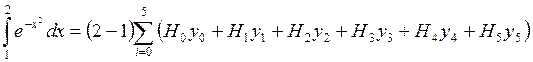По свойствам коэффициентов Ньютона-Котеса

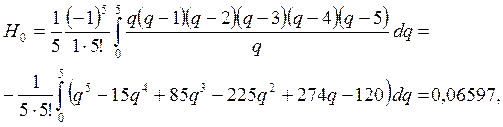
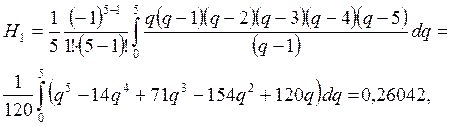
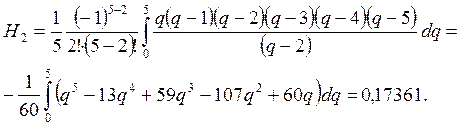
Далее вычислим значения подынтегральной функции в точках , i = 0, 1, 2, 3, 4, 5.

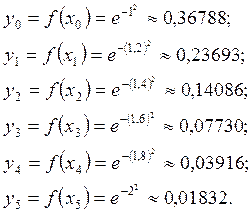
Учитывая свойства коэффициентов Ньютона-Котеса, можем записать

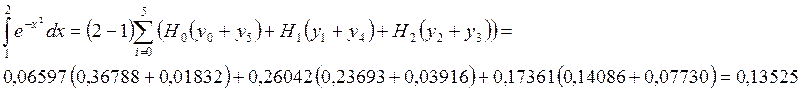
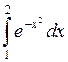 = 0,13525.

Формула Гаусса

Пусть необходимо вычислить интеграл вида .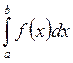

Квадратурная формула Гаусса имеет вид:

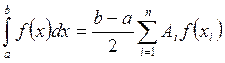,                                                                 (2)

где

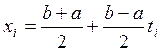 (i = 1, 2,…, n),                                                               (3)

 - нули полинома Лежандра  , т. е. .

Для коэффициентов  и узлов  существуют справочные таблицы.

Формула Гаусса обеспечивает наивысшую точность в том смысле, что для полиномов степени не выше  она точна.

Таблица 1       

n	i	ti	Ai
1	1	0	2
2	1; 2	0,57735027	1
4	3	1; 3 2	0,77459667 0
5	1; 5 2; 4 3	0,90617985  0,53846931 0	0,23692688 0,47862868 0,56888889
6	1; 6 2; 5 3; 4	0,93246951  0,66120939  0,23861919	0,17132450 0,36076158 0,46791394
7	1; 7 2; 6 3; 5 4	0,94910791  0,74153119  0,40584515  0	0,12948496 0,27970540 0,31183006 0,41795918
8	1; 8 2; 7 3; 6 4; 5	0,96028986  0,79666648  0,52553242  0,18343464	0,10122854 0,22238104 0,31370664 0,36268379

Пример.

Применяя квадратурную формулу Гаусса, вычислить интеграл .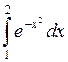

Разобьем интервал [1, 2] на n = 5 точек и для вычисления интеграла воспользуемся полиномом Лежандра 5-й степени .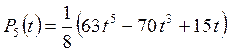

Делаем замену переменной ,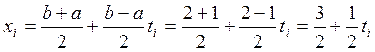

где  - корни (нули) полинома Лежандра  , т. е. .

Из таблицы 1 возьмем значения корней  и коэффициентов :

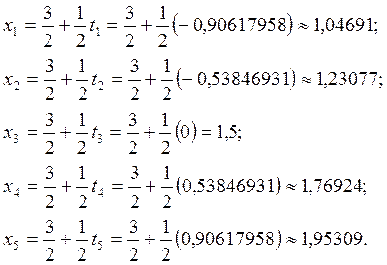
Далее вычислим значение подынтегральной функции :

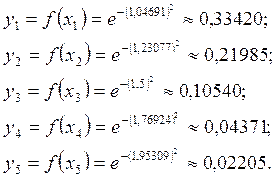
Согласно формуле (2):

.

________________________________________________________________________________

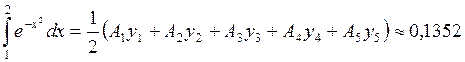Вычислить интегралы:

                            

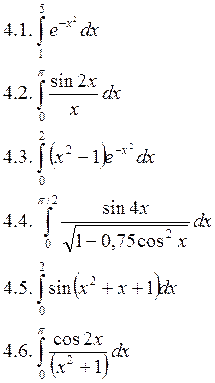
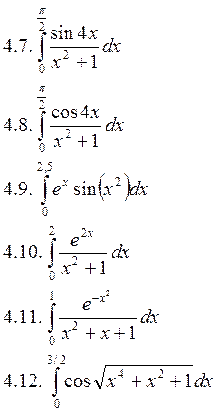
5. Приближенное решение обыкновенных дифференциальных уравнений

Обыкновенным дифференциальным уравнением порядка n называется уравнение

,                                                 (1)

которое связывает независимую переменную x, искомую функцию  и ее производные . Общее решение уравнения (1) зависит от n произвольных постоянных. Большое значение имеют два рода задач, связанных с определением частных решений уравнения (1): задачи Коши, или задачи с начальными условиями, и граничные задачи. Задача Коши состоит в нахождении решения , удовлетворяющего начальным условиям

,                                        (2)

где  - заданные числа. Условия (2) для задачи Коши задаются в одной точке . Для граничных задач дополнительные условия задаются не в одной, а в нескольких точках.

Численные методы используются в задачах, имеющих единственное решение (т.е. корректно поставленных). В некоторых случаях условий корректности может оказаться недостаточно. Необходимо, чтобы задача была хорошо обусловлена (устойчива), т. е. малые изменения в задании исходных данных приводили к достаточно малым изменениям искомого решения.

Метод Эйлера

Метод Эйлера является одним из самых простых методов численного решения дифференциальных уравнений. Недостатком его является сравнительно низкая точность.

Пусть дано дифференциальное уравнение

                                                                               (3)

с начальным условием

.                                                                             (4)