Сравнительный подход. Идентификация подлежащего оценке объекта недвижимости. Определение поправки на износ по методу прямого анализа характеристик, страница 12

Введение поправки на масштаб.             При оценке следует учитывать тот факт, что при прочих равных условиях цена единицы площади больших значений ниже, чем маленьких, причем разброс на одном сегменте рынка составляет около 7%. Этот момент при сравнении аналогов корректируется введением поправки на масштаб (поправка Мисовца).

            В результате анализа выборки из 16 объектов была выявлена линейная зависимость между ценой 1 м² площади здания (результативный признак) и общей площадью здания (факторный признак). Для определения коэффициента  была построена следующая таблица:

            Подставляя рассчитанные в таблице значения в уравнения расчета коэффициентов, получим:

.

.

            Уравнение регрессии имеет вид:

.

            Далее необходимо оценить тесноту корреляционно-регрессионной связи. Для этого используем коэффициент Фехнера, который на основе анализа отклонений значений факторного и результативного признаков от их средних величин запишется в виде:

,

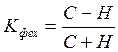где С – сумма совпадающих по знакам пар отклонений  и от их средних значений;

       Н – сумма не совпадающих  по знакам пар отклонений  и от их средних значений.

            Коэффициент Фехнера колеблется в пределах от –1 до +1. Связь считается тесной, если значение этого коэффициента по модулю не ниже 0.7. При значениях коэффициента по модулю меньше 0.5 нельзя говорить о репрезентативной зависимости между факторным и результативным признаками. Знак коэффициента говорит о том, является ли зависимость прямой или обратной, – если коэффициент положителен, результативный фактор возрастает с возрастанием факторного, если коэффициент отрицателен, результативный признак убывает с возрастанием факторного.

            Для нашего примера:

,

что говорит о тесной отрицательной связи. Это подтверждается и на практике  - с ростом площади зданий падает цена одного квадратного метра.

            Поправка Мисовца является относительной денежной. Она может быть рассчитана как разница цен квадратного метра зданий разных площадей и равна при этом произведению разницы в площадях оцениваемого и сопоставимого объектов на коэффициент регрессии b (применительно к данной поправке он называется фактором Мисовца) (Ф_м):