Сравнительный подход. Идентификация подлежащего оценке объекта недвижимости. Определение поправки на износ по методу прямого анализа характеристик, страница 11

Поправки в процентах – это суммы, прибавляемые и вычитаемые от продажной цены сопоставимого объекта. Их можно сложить (вычесть) друг с другом, а затем внести суммарную поправку в цену продажи. Или можно вносить каждую поправку отдельно одну за другой, каждый раз корректируя цену аналога.

Если поправки вводятся на кумулятивной основе, то каждая поправка добавляется и вычитается из 100%. Затем коэффициенты могут быть перемножены, или каждая поправка вносится отдельно одна за другой в цену аналога.

Расчет поправок статистическими методами.

            Статистические методы основаны на анализе значительных выборок данных из базы. Наиболее распространенным является метод корреляционно-регрессионного анализа, который основан на предположении о существовании подвергающейся формализации зависимости между вариацией цен объекта и вариацией тех или иных характеристик.

            Как правило, рассматриваются достаточно простые виды корреляционных зависимостей:

·  линейная ;

·  квадратичная

·  обратная (гиперболическая) ;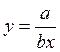

·  степенная .

Эти формулы описывают парную корреляционную связь. Коэффициенты в этих формулах рассчитываются методом наименьших квадратов (МНК), основанном на том, что теоретически рассчитанные значения результативного признака (у) должны минимально отличаться от эмпирических значений.

Исходное условие МНК для прямой линии имеет вид:

.

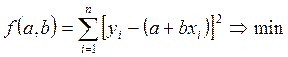Для отыскания значений параметров  и , при которых  принимает минимальное значение, частные производные функции приравниваем к нулю  и преобразуем полученные уравнения, которые называются нормальными уравнениями МНК для прямой:

;

.

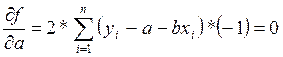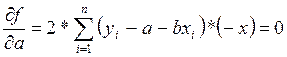Отсюда, система нормальных уравнений имеет вид:

.

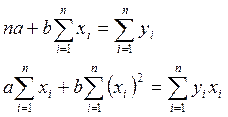Решая эту систему, получим:

,

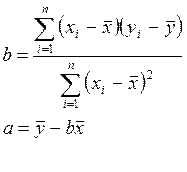где  и  - средние величины факторного и результативного признаков соответственно;  - порядковый номер элемента выборки;  - количество элементов выборки.

            Для определения формулы множественной корреляции необходимо решать системы, число уравнений в которых равно числу коэффициентов при факторных признаках и свободных членах.

            Имея формулу зависимости результативного признака от факторного, можно на ее основе рассчитать поправки на значения факторных признаков.