Теория принятия и реализация управленческих решений: Методические указания к выполнению практических работ, страница 5

3.  Поставив мысленный эксперимент по изменению нагрузки на линейку, как в направлении вверх, так и в направлении вниз, обоснуйте вид графика рис. 1, в. Для этого определите, в какой точке графика будет находиться система

·  при отсутствии нагрузки;

·  при малой нагрузке, направленной вниз;

·  при большой нагрузке, направленной вверх;

·  в состоянии с прогибом вниз без нагрузки;

·  в состоянии с прогибом вниз с небольшой нагрузкой, направленной вверх;

·  в состоянии с прогибом вниз с небольшой нагрузкой, направленной вниз.

4.  Постройте на рис. 1, в траекторию движения системы из состояния, показанного на рис 1,а (без груза) при увеличении груза (усилие направлено вниз). Найдите ситуацию, при которой происходит резкое изменение выходной величины при небольшом изменении входной.

5.  По графику рис 1, в определите, сколько возможно ситуаций, когда малое входное воздействие приводит к сильному изменению выходной величины. Все эти ситуации именуются катастрофами.

Выводы по части 1

Исследуемая система имеет две точки устойчивого равновесия и точку неустойчивого равновесия. Наблюдаемое катастрофическое поведение системы обусловлено тем, что система стремится уменьшить свою энергию (в данном случае – потенциальную энергию сжатой пружины).

Итак, для появления катастрофы требуется:

·  система, имеющая характеристику, аналогичную показанной на рис. 1, в;

·  способность данной системы изменять свою внутреннюю энергию в зависимости от внешнего воздействия;

·  внешнее воздействие определенного направления.

1.5. Модель двумерной системы

Такая модель имеет два входных воздействия. Во многих литературных источниках приводится пример исследования нарушений режима в тюрьме. Согласно исходной гипотезе, интенсивность беспорядков является функцией от напряженности и разобщенности заключенных. Теоретически эту зависимость можно представить в виде графика рис. 2.

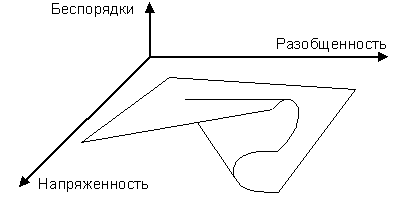
Рис. 2. Зависимость интенсивности беспорядков
от напряженности и разобщенности

Такой график называется сборкой. Пусть «идеальным» исходным состоянием является точка поверхности, наиболее близкая к началу координат, когда разобщенность и напряженность малы. При этом происходят умеренные беспорядки.

1.6. Задание, часть 2

1.  Предложить способ оценки разобщенности и напряженности, используя знания, полученные при изучении дисциплины «Маркетинговые исследования».

2.  Показать траектории движения объекта исследования на графике от начальной точки

·  при возрастании разобщенности до максимального значения, затем – напряженности до максимального значения;

·  при возрастании напряженности до максимального значения, затем – разобщенности до максимального значения.

3.  Проследить дальнейшую траекторию из полученных точек для первого случая – при уменьшении разобщенности, для второго при уменьшении напряженности.

4.  Перечислить особенности поведения системы исходя из полученных результатов.

1.7. Результаты исследований, проведенных в тюрьме

Реально проведенные эксперименты показали следующее.

·  Имеются области, где поведение объекта исследования неустойчиво, но их форма не согласуется с теоретически предсказанной.

·  Для объяснения результатов приходится привлекать достаточно сложные дополнительные допущения.

Таким образом, теория катастроф имеет скорее качественную ценность. В частности, с ее помощью можно объяснить такие явления истории, как неожиданные переселения народов на новые территории при отсутствии войн и катаклизмов. Теория катастроф допускает, что постепенные изменения входных воздействий или состояния системы (в данном случае, например, климата или плодородия почвы) могут приводить к резкому изменению выходной величины. Из нее вытекает возможность скачков – «катастроф».