Линейное математическое программирование, страница 9

4.4. Определение оптимального решения.

Рассмотрим на примере  графический метод определения оптимального решения ЗЛП – max. или  min. значения целевой функции.

Пример 4.4.

Найти такие неотрицательные значения переменных, которые удовлетворяют ограничениям

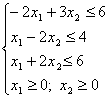
и оптимизируют функцию цели , т.е. обеспечивают ей максимальное или минимальное значения.

Вводим дополнительные переменные, чтобы преобразовать неравенства в равенства.

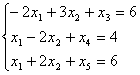
Т.к. определяется область допустимых решений, то все переменные должны быть неотрицательными, т.е.

Строим многоугольник допустимых решений (рис. 4.8)

 

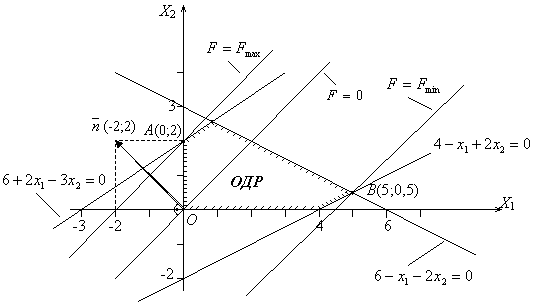
Рис.4.8

Введём в рассмотрение линии уровня функции цели. Линии уровня функции цели – линии, на которых функция цели имеет постоянное значение. В рассматриваемом случае уравнение линий уровня имеет вид . Это параллельные прямые, т.к. коэффициенты при переменных в уравнении не изменяются, а меняется только постоянная. Все они направлены перпендикулярно вектору нормали . Линии уровня обладают тем свойством, что в направлении вектора нормали их величина возрастает, а в противоположном направлении – убывает. Линия уровня, проходящая, через начало координат, будет иметь нулевое значение, проходящая через точку А(0;2) – max, проходящая через точку В(5;0,5) – min.

Заметим, что оптимальные значения целевой функции получены в угловых точках многогранника решений.

Отметим общие свойства решений ОЗЛП.

1.Оптимальное решение ОЗЛП, если оно существует, не может лежать внутри ОДР, а только на её границах.

2.Если границей ОДР для линии уровня функции цели является угловая точка, то функция цели принимает единственное оптимальное решение.

3.Если линия уровня функции цели совпадает с одной из ребер многогранника допустимых решений, задача имеет бесконечное множество оптимальных решений.

4.ОЗЛП может не иметь решений в следующих случаях:

1.Когда система ограничений несовместна. В этом случае не существует ОДР.

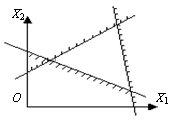
Рис. 4.9.

2.Если и существует ОДР, но она не ограничена.

 

Рис. 4.10.

5.Симплексный метод решения ОЗЛП

Симплексный метод – метод аналитического определения оптимального значения целевой функции. Идея метода состоит в последовательном переходе от одной вершины многогранника допустимых решений к соседней, в которой функция цели принимает лучшее (по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет решение).

Для реализации симплексного метода необходимо:

 1.Найти первоначальное допустимое базисное решение (опорный план);

 2.Обеспечить переход от одного решения к другому лучшему;

 3.Проверить каждое решение на соответствие критерию оптимальности.

При решении задачи симплексным методом система ограничений и целевая функция должны быть представлены в симплексной форме, а именно:

 1) система ограничений должна быть представлена в виде уравнений;

 2) все свободные члены уравнений должны быть неотрицательными;