Линейное математическое программирование, страница 15

Из таблицы следует, что функцию цели уменьшить больше нельзя, т.к. оба коэффициента при неосновных переменных положительны. Это условие определяет оптимальное значение функции цели, которое в рассматриваемой задаче равно

Критерий оптимальности при определении минимума линейной функции.

Если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновные переменных, то найденное решение оптимально.

5.3. Определение первоначального допустимого базисного решения.

Симплексный метод применяется только в случае, когда первоначальное базисное решение является допустимым. В случае, когда на первом шаге получается недопустимое базисное решение, его следует исключить и найти допустимое решение.

Существует два метода определения допустимых опорных планов – метод итераций и метод искусственного базиса. 

Метод итераций.

В методе итераций используется тот же симплексный метод. Сначала выбирают разрешающую строку, в которой свободный член является отрицательным. Затем по минимуму отношения свободного члена в разрешающей строке к отрицательным коэффициентам при свободных переменных определяется разрешающий столбец. Если таких строк с отрицательными свободными членами несколько, для каждой из них следует проводить  один шаг симплекс – метода.

Замечание. Если в задаче окажется строка с отрицательным свободным членом, а все коэффициенты при свободных переменных положительны, то такая задача решения не имеет.

Рассмотрим метод итераций на примере.

Пример 5.3

Найти минимальное значение целевой функции  при ограничениях

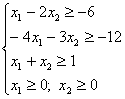
Преобразуем систему ограничений – неравенств в систему ограничений – равенств

Представим эту систему ограничений и функцию цели в симплексной форме

           

Базисными являются переменные х₃; х₄; х₅, переменные х₁, х₂ – свободные.

Первое базисное решение Х₁(0;0;6;12;-1) является отрицательным.

Заполним симплекс-таблицу 5.6

Третью строку выбираем в качестве разрешающей, т.к. она содержит отрицательный свободный член. За разрешающий столбец можно выбрать любой х₁ или х₂, т.к. коэффициенты при них отрицательные. Выбираем столбец х₁.

Таблица 5.6