Линейное математическое программирование, страница 3

Стоимость единицы веса корма I и I I, соответственно равны 3 и 4 у.е.

Необходимо составить рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

Экономическо-математическая модель задачи.

Обозначим через х₁ и х₂ – количество кормов I и II, входящих в рацион питания.

Тогда этот рацион будет включать

                                 3х₁ + х₂ весовых единиц питательного вещества S₁

                                 х₁ + 2х₂ весовых единиц питательного вещества S₂

                                 х₁ + 6х₂ весовых единиц питательного вещества S₃

Так как каждого питательного вещества в рационе должно быть не менее 9, 8 и 12 единиц, то приходим к системе

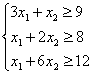                                                                                                  (1.7)

Переменные х₁ и х₂ должны отвечать условиям

                                                                                                            (1.8)

            Функция цели, определяющая минимальные затраты на приобретение кормов, имеет вид

                                                                             (1.9)

            В общем виде задача по приготовлению рациона питания, включающего n видов корма, имеет вид:

                                             (1.10)

            При                                                                         (1.11)

и                                                                    (1.12)

Здесь х_j – весовое количество j-того корма в рационе;

    а_ij – содержание i-того питательного вещества в j-том корме i = (1, 2, …, m), j = (1, 2, …, n);

    b_i – необходимый минимум содержания i-того питательного вещества в рационе;

    c_j – стоимость единицы корма j-того тина.

            1.3. Задача об использовании мощностей (задача о загрузке оборудования).

            Предприятию задан план выпуска продукции по времени и номенклатуре. Требуется за время Т выпустить n₁ , n₂ ,…, n_к единиц продукции по номенклатуре Р₁, Р₂, , … , Р_к. Продукция производится на станках S₁, S₂,…, S_m. Для каждого станка известна производительность a_ij – количество единиц продукции Р_j, которое можно произвести на станке Si в единицу времени.

            Необходимо составить такой план загрузки оборудования, чтобы затраты на производство всей продукции были минимальными.

            Экономическо-математическая модель задачи.

         Обозначим х_ij – время , в течении которого станок Si загружен изготовлением продукции Р_j.

            i = 1, 2, … , m ;   j = 1, 2, … , к.

            Так как время работы каждого станка ограничено и не превышает Т, то имеют место неравенства

                                                                                  (1.13)