Линейное математическое программирование, страница 5

Для группы х₁, х₄                                                          Для группы х₂, х₃

                                                   

Для группы х₂, х₄                                                          Для группы х₃, х₄

                                                             

Таким образом, из 6 возможных групп базисных переменных только три группы, составленные из переменных х₁,х₂; х₁,х₃;  х₁,х₄, являются таковыми.

2. Найдём бесконечное множество решений для группы базисных переменных х₁,х₂.

В системе уравнений разделяем переменные. Слева от знака равенства оставляем базисные переменные, справа записываем неосновные переменные и свободные члены уравнений.

;

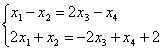
Т.к. х₃ и х₄ – свободные переменные, положим х₃ = с₁; х₄ = с₂.

Тогда  , , , , где ,

3.Найдём базисные решения.

Базисное решение для группы базисных переменных х₁ и х₂ ищется при условии, что х₃ = 0, х₄ = 0.

; ;  – 1-е  базисное решение.

Базисное решение для группы базисных переменных х₁ и х₃. ищется при условии, что х₂ = 0, х₄ = 0.

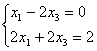
; ;  – 2-е  базисное решение.

Базисное решение для группы базисных переменных х₁ и х₄ ищется при условии, что х₂ = 0, х₃ = 0.

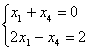
; ;  – 3-е  базисное решение.

4. Допустимыми базисными решениями являются точки  и , недопустимым-.

▲

3.Основная задача линейного программирования (ОЗЛП)

Задача с ограничениями в виде равенств называется ОЗЛП. Она ставится следующим образом.

Имеется n переменных х₁, х₂, …, х_n, входящих в систему m уравнений (2.1).

Требуется найти такие неотрицательные значения этих переменных, которые удовлетворяли бы ограничениям – уравнениям, при которых линейная функция, являющаяся функцией цели или целевой функцией  принимала бы оптимальное значение (min. или max.)