Линейное математическое программирование, страница 25

В каждой клетке для каждой пары “поставщик - потребитель” указаны коэффициенты затрат на перевозку груза от i-того поставщика к j-тому потребителю.

Задача ставится следующим образом:

Найти объёмы перевозок груза для каждой пары “поставщик-потребитель” чтобы:

    1. запасы груза поставщиков были реализованы;

    2. спросы всех потребителей были удовлетворены;

    3. суммарные затраты на перевозку были минимальными.

7.1. Экономико-математическая модель задачи

Обозначим через х_ij-объём перевозки от i-того поставщика к j-тому потребителю и назовём его поставкой клетки (і, j).

Чтобы запасы груза поставщиков были реализованы, необходимо составить уравнение баланса для каждой строки таблицы поставок, т.е.

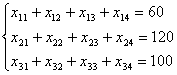                                                                            (7.1)

Для того чтобы спрос каждого потребителя был удовлетворён, подобные уравнения баланса составим для каждого столбца таблица поставок

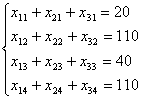                                                                                                 (7.2)

Очевидно, что объём перевозимого груза не может быть  отрицательным, поэтому следует дополнительно предположить, что

                    х_ij (і = 1,2,3;  j = 1,2,3,4).

Суммарные затраты F на перевозку груза  должны быть минимальными.

 

Особенности экономико-математической модели транспортной задачи:

1.  Система ограничений есть уравнение;

2.  Коэффициенты при переменных системы ограничений равны единице или нулю;

3.  Каждая переменная входит в систему ограничений два раза – один раз в систему (7.1) и один раз – в систему (7.2).

В рассматриваемой транспортной задаче суммарные запасы груза поставщиков (280) равны суммарному спросу  потребителей (280). Такие транспортные задачи называются закрытыми. Если обозначить через m – число поставщиков, через n – число потребителей, то ранг системы ограничений будет равен m + n – 1.

Так же как и при решении любой задачи  ЛП  при решении Т.З. переменные х_ij должны быть разбиты на основные (базисные) и неосновные (свободные). Базисная переменная х_ij в транспортной задаче равна поставке в клетку с номером (і;j), которая называется базисной клеткой или заполненной клеткой. Число базисных переменных (базисных клеток) в закрытой Т.З. должно быть равно рангу системы, т.е. числу m + n – 1. Остальные незанятые (пустые) клетки соответствуют свободным (неосновным) переменным.

На первом шаге решения Т.З. как и в симплексном методе необходимо  найти исходное базисное распределение поставок (опорный план).

7.2. Определения первоначального базисного распределения поставок (опорного плана)

Производится двумя методами – методом “северо-западного угла” и методом наименьших затрат.

7.2.1. Метод “северо-западного угла”

            Заключается в том, что на каждом шаге заполняется левая верхняя клетка (северо-западная). При этом в клетку производится максимально возможная поставка – либо полностью обеспечивается сырьем потребитель, либо полностью вывозится груз поставщика. Процедура продолжается до тех пор, пока полностью исчерпаются запасы и будут обеспечены сырьем все потребители.

Пример 7.1.

Найти первоначальное базисное распределение поставок для транспортной задачи, определяемой таблицей поставок (таблица 7.1)

Таблица 7.2