Линейное математическое программирование, страница 21

Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.

Обозначим через х₁  и  х₁ количество машин соответственно типа А и В, через F – общую производительность.

Тогда математическая модель имеет вид:           

при ограничениях:

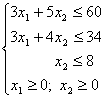
х₁; х₂ – целые числа.

Приведём задачу к ограничениям в виде уравнений, введя дополнительные переменные

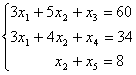
Решим задачу симплексным методом. Представляем систему ограничений в табличной форме (таблица 6.1)

Таблица 6.1

Первое решение Х₁(0; 0; 60; 34; 8) допустимое, но не оптимальное т.к. в функции цели оба коэффициента при свободных переменных положительные. Для увеличения F можно переводить в основные либо х₁ либо х₂. Выберем переменную х₂, имеющую больший коэффициент. Этим выбором определяется разрешающий столбец (выделен). Разрешающую строку выбираем из условия  (выделена). Переводим методом симплексного преобразования переменную х₂ в основные, а переменную х₅ – в неосновные (таблица 6.2)

Таблица 6.2