Линейное математическое программирование, страница 6

Значения переменных, при которых целевая функция принимает оптимальное значение, называется оптимальным решением или оптимальным планом.

Задача ЛП с ограничениями в виде неравенств любого вида “≥0”,  “ ≤0” сводится к ОЗЛП на основании следующей теоремы.

            Теорема

            Всякому решению , , …,  неравенства  соответствует определенное решение , , …, ,  уравнения , где

            Эта теорема позволяет преобразовать систему ограничений–неравенств в систему ограничений–равенств.

           

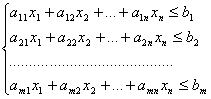
            В систему ограничений-неравенств для того, чтобы уравнять левые и правые части, нужно в левую часть каждого неравенства ввести дополнительные неотрицательные переменные , , …, .

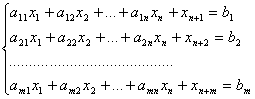
В случае неравенств вида “≥” в левую часть каждого неравенства нужно вводить дополнительные переменные со знаком минус.

Пример 3.1

В задаче ЛП с переменными х₁, х₂, х₃, х₄ и ограничениями вида

           

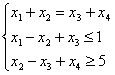
минимизируется функция .

Требуется привести задачу к ОЗЛП.

▼

Введём дополнительные переменные х₅ и х₆ во 2-е и 3-е уравнение с соответствующими знаками.

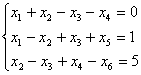
   Целевая функция не изменяется.

            ▲

4. Геометрическая интерпретация решения ОЗЛП

4.1.Определение области решения неравенств.

Рассмотрим сначала задачу по определению множества решений неравенства. Теорема

Множество решений неравенства с двумя  переменными  является одна из двух полуплоскостей, на которые вся плоскость делится прямой , включая и эту прямую, а другая плоскость с той же прямой есть множество решений неравенства .

Пример 4.1.

Найти область решений неравенств

1. 

2. 

▼

1. Строим прямую  по отрезкам, отсекаемым прямой на осях координат.

      при

               

Прямая делит плоскость на две полуплоскости. Для определения этой полуплоскости возьмём контрольную точку и подставим её в неравенство. Если неравенство выполняется в контрольной точке, оно выполняется во всех точках полуплоскости, которой принадлежит контрольная точка. Если не выполняется в контрольной точке, оно выполняется в другой полуплоскости. Если прямая не проходит через начало координат, в качестве контрольной точки используется  начало координат. Если прямая проходит через начало координат, берётся точка, не лежащая на прямой.