Линейное математическое программирование, страница 10

 3) система ограничений содержит m уравнений и столько же базисных переменных;

 4) коэффициенты при базисных переменных в системе ограничений должны быть равны единице.

В общем виде система ограничений выглядит так:

 5) целевая функция должна быть выражена через неосновные переменные и представлена в виде

5.1. Отыскания максимума линейной функции

Рассмотрим симплексный метод на примере задачи, которая была решена графическим путём в примере 4.4.

Пример 5.1

Найти max функции цели  при ограничениях:

1. Представляем систему ограничений и функцию цели в симплексной форме

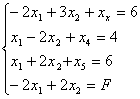                                                                                      (5.1)

2. Выбираем базисные переменные и исходное допустимое базисное решение (опорный план).

            Для определения первоначального базисного решения разобьем переменные на две группы – базисные (основные) и неосновные. В рассматриваемой задаче в качестве базисных переменных можно взять переменные х₃, х₄, х₅, т.к. определитель, составленный из коэффициентов при этих неизвестных не равен нулю. Действительно

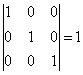
При выборе базисных переменных на первом шаге не обязательно составлять определитель из их коэффициентов и определять его значение. Достаточно воспользоваться следующим правилом:

В качестве базисных переменных на первом шаге следует выбирать такие m переменных, каждая из которых входит только в одно уравнение системы ограничений, при этом нет таких уравнений, в которые не входит ни одна из этих переменных. При этом, если знаки этих переменных такие же, как и знаки соответствующих свободных членов уравнений, то полученное таким образом базисное решение будет допустимым.

Дополнительные переменные х₃, х₄, х₅ удовлетворяют этому правилу.

Т.к. переменные х₁ и х₂ являются неосновными, то положив х₁ = 0 и х₂ = 0, получаем из системы уравнений (5.1) первоначальное базисное решение х₁ (0; 0; 6; 4; 6).

Это решение является допустимым. Оно соответствует угловой точке многоугольника (рис.4.8.), находящейся в начале координат.

Т.к. решения допустимые, нельзя отбросить возможность того, что оно оптимально. При решении х₁ значение целевой функции равно . Из выражения для функции цели  видно, что ее можно увеличить за счет увеличения переменной х₂, которая входит в выражение для функции цели с положительным коэффициентом. Увеличить переменную х₂ – это значит перейти к другому базисному решению, в которой переменная х₂ будет основной, т.е. будет принимать не нулевые, а положительные значения. Если функция цели содержит несколько неосновных переменных с разными по величине и знаку коэффициентами, то для перевода в основные следует выбирать ту переменную, при которой коэффициент имеет наибольшее положительное значение.

Таким образом ставится задача о «переразрешении» системы уравнений-ограничений относительно новых базисных переменных. Эту операцию удобно осуществлять в табличной форме, в которой удобно представить систему правил по «переразрешению» системы уравнений.

Табличный алгоритм замены базисных переменных

1. Представляем исходную систему уравнений-ограничений (5.1) в табличной форме (таблица 5.1)