Для выполнения плана выпуска по номенклатуре необходимо чтобы выполнялись следующие равенства
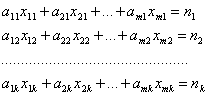 (1.14)
(1.14)
Кроме этого быть xij ≥ 0 (1.15)
Затраты на производство всей продукции выразятся функцией
![]() (1.16)
(1.16)
Нужно найти такое решение х (х11, x12 , …, xmk), удовлетворяющее системам (1.13), (1.14) и условию (1.15), при котором функция цели (1.16) принимает минимальное значение.
2. Cистемаm линейных уравнений с n переменными
В задачах Л.П. принципиальное значения имеют системы линейных уравнений, в которых число переменных n больше числа уравнений m .
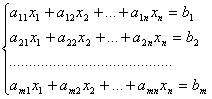 (2.1)
(2.1)
n > m
Если все уравнения независимы, то ранг матрицы, составленной из коэффициентов при неизвестных, равен числу уравнений r = m. Тогда при условии совместности системы (когда ранг матрицы системы равен рангу расширенной матрицы) поскольку n > m = r, система имеет бесконечное множество решений.
При поиске этих
решений определяют группы m переменных, которые
называют основными или базисными. Число групп базисных переменных определяется
из условия неравенства нулю определителя, составленного из коэффициентов при
этих неизвестных. Число групп базисных переменных не превышает числа сочетаний
из n элементов по m, т.е. ![]() .
.
Остальные m-n переменных называются неосновными или свободными.
Решение, полученное при условии, что все свободные переменные равны нулю, называются базисным решением. Базисное решение может быть допустимым или недопустимым. Допустимым базисным решением (его ещё называют опорным планом) есть решение, в котором значения всех переменных неотрицательны. Недопустимым является базисное решение, в котором значение хотя бы одной переменной отрицательное.
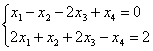
найти:
1) все группы базисных переменных;
2) бесконечное множество решений, для одной из групп базисных переменных;
3) все базисные решения;
4) допустимые и недопустимые базисные решения.
▼
1. Определим общее число возможных групп основных (базисных) переменных.
![]()
Возможные группы основных переменных следующие
х1,х2; х1,х3; х1,х4; х2,х3; х2,х4; х3,х4;
Среди этих групп переменных базисными будут те, для которых определители, составленные из коэффициентов при этих неизвестных не равны нулю.
Для группы х1, х2 Для группы х1, х3
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.