Линейное математическое программирование, страница 17

Полученное решение х₃(3;0;9;0;2) является оптимальным, т.к. коэффициенты при неосновных переменных х₂ и х₄ являются положительными, что является критерием оптимальности целевой функции при поиски ее минимума. Целевая функция  при х₂ = х₄ = 0 равна

Метод искусственного базиса

Состоит в следующем. В каждое уравнение, дающее отрицательную компоненту в базисном решении, вводится  искусственная неотрицательная переменная y₁, y₂…y_m, которая имеет тот же знак, что и свободный член в правой части уравнения. В первую симплекс-таблицу заносятся искусственные переменные. Вводится  вспомогательная целевая функция f = 0 при условии, когда y₁ = y₂ = … y_m = 0. Путём перевода искусственных переменных из основных в неосновные достигается допустимое решение. После этого производится оптимизация обычным методом.

Пример 5.4.

            Решим задачу, рассмотренную в примере 5.3

Определим допустимое решение методом искусственного базиса.

            Найти

при ограничениях

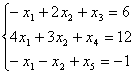
В последнее уравнение, определяющее недопустимое значение базисной переменной х₅ = –1 вводим искусственную переменную y₁ с тем же знаком, что и свободный член. Получаем систему ограничений

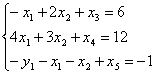        или    

в которой все базисные переменные х₃; х₄; y₁ имеют допустимые значения.

            Вспомогательная функция цели F = – y₁.

            Составим первую симплекс-таблицу

                                                                                                                         Таблица 5.9