Линейное математическое программирование, страница 8

Рис.4.6

Решением системы m линейных неравенств с n переменными является выпуклая многогранная область в n-мерном пространстве.

4.3. Множество допустимых решений системы m линейных уравнений с n переменными.

Допустимым является такое решение, при котором все найденные значения переменных х₁, х₂, …, х_n неотрицательны.

Теорема.

Множество всех допустимых решений совместной системы m линейных уравнений с n переменными (m < n) является выпуклым многогранником (выпуклой многогранной областью) в n-мерном пространстве.

Пример 4.3.

Построить множество допустимых решений системы уравнений

            ▼

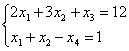
Построить графически область допустимых решений системы уравнений с четырьмя переменными не представляется возможным.

В случае, когда разность между числом переменных n и числом уравнений m равна двум (m–n=2) поступают следующим образом. Разбивают переменные на основные (базисные) и неосновные (свободные). Например, переменные х₃ и х₄ можно взять за базисные, т.к. определитель, составленный из коэффициентов при этих переменных отличен от нуля. Действительно:

Тогда х₁ и х₂ будут свободными.

В таком случае вместо определения множества решений системы уравнений определяется множество значений их неосновных переменных. Выполнить это возможно, т.к. их всего две.

Выразим основные переменные через неосновные

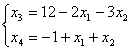
Т.к. рассматриваются допустимые значения переменных, т.е. х₁ ≥ 0; х₂ ≥ 0; х₃ ≥ 0; х₄ ≥ 0, то

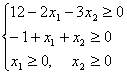
Решаем графически систему неравенств

 

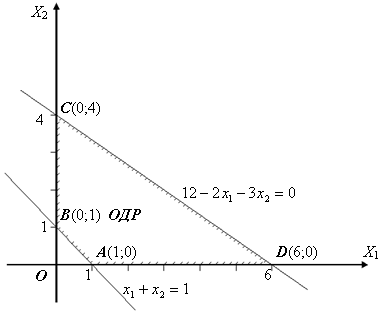Рис.4.7

Т.к. , то ОДР системы неравенств расположена в первой четверти. Решением системы неравенств является выпуклый четырехугольник с точками при вершинах  А(1;0), В(0;1), С(0;4), D(6,0) (рис.4.7).

В рассматриваемом примере геометрические построения проведены в плоскости двух неосновных переменных х₁ и х₂. Но т.к. каждой паре неосновных переменных соответствуют определённые значения основных переменных х₃ и х₄, а следовательно только одно решение системы уравнений, то каждой точке четырёхугольника решений в плоскости неосновных переменных будет соответствовать точка многогранника допустимых решений в четырехмерном пространстве.

Между угловыми точками множества допустимых решений системы линейных уравнений и допустимыми базисными решениями существует взаимно-однозначное соответствие.

Найдём допустимые базисные решения для рассмотренного примера.

Для точки А(1;0):            Х₁(1;0;10;0) – первое базисное решение.

Для точки В(0;1):                          Х₂(0;1;9;0) – второе базисное решение.

Для точки С(0;4):             Х₃(0;4;0;3) – третье базисное решение.

Для точки D(6,0):             Х₄(6;0;0;5) – четвертое базисное решение.