p(A) = p(Н1)∙р(А/H1) + p(Н2)∙р(А/H2) +…+ p(Нn)∙р(А/Hn)
Это и есть формула полной вероятности
Пример: Пусть на экзамен первым вошли 6 студентов, среди них 2 отличника (могут сдать экзамен с вероятностью 0,9), 3 хорошиста (вероятность 0,8) и 1 троечник (вероятность 0,3). Какова вероятность сдачи экзамена первых случайно выбранных студента?
Дано: 3 гипотезы: Н1 (отличник), Н2 (хорошист), Н3 (троечник)
Даны условные вероятности р(А/Н1) = 0,9; р(А/Н2) = 0,8; р(А/Н3) = 0,3
Определим вероятности наступления гипотез:
р(Н1) = 2/6 = 1/3; р(Н2) = 3/6 = 1/2; р(Н3) = 1/6
Определим искомую вероятность по формуле полной вероятности:
р(А) = 1/3∙0,9 + 1/2∙0,8 + 1/6∙0,3 = 0,75
Формула полной вероятности позволяет определить вероятность наступления события, связанных с наступлением некоторых гипотез, вероятность которых a’priori известна.
2.14 Формула Байеса
На практике во многих случаях задача определения вероятности наступления события с одной из гипотез часто переформулируется таким образом, что после того как событие наступило можно уточнить вероятность наступления каждой из гипотез, которые ранее были заданы a priory.
Теперь можно решить обратную задачу, состоящую в том, что если событие реализовалось, то вместе с ним реализовалась одна из гипотез Нi и, следовательно, появляется возможность уточнить вероятность наступления той или иной гипотезы уже после опыта Apasteriry.Эта задача решается по формуле Байеса:
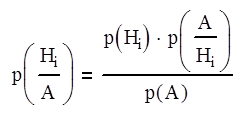
где i – текущий номер (i=1,2,3,…)
Формула Байеса читается следующим образом: условная вероятность того, что реализовалась гипотеза Нi при условии, что А произошло равно произведению вероятности этой гипотезы на условную вероятность того, что событие А произойдет с этой гипотезой Нi и деленное на вероятность наступления события р(А), которое находится по формуле полной вероятности.
Рассмотрим продолжение примера из предыдущей лекции.
Уточним вероятность наступления гипотезы после сдачи экзамена:
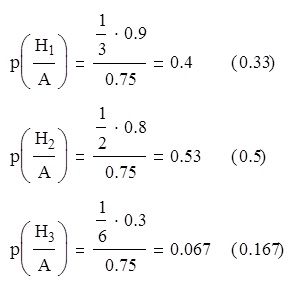
Следовательно формула Байеса позволяет уточнить условную вероятность наступления гипотезы Нi после проявления опытов, в результате которых событие А произошло.
11 Формула Бернулли
В ряде случаев при многократном проявление опытов требуется вычислить вероятность того, что событие произойдет m раз в n испытаниях. Пусть событие А будем называть успехом, если оно состоялось, а если нет – неудача. Тогда вероятность наступления события называется успешным равна р(А), а неудачным – q(A). При этом предполагаем, что испытание не зависит от совокупности и вероятности проявления каждого из событий одинакова. Тогда вероятность успешных событий:
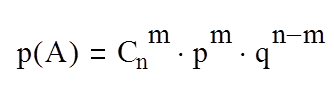
где Сnm – число сочетаний; рm – вероятность получение успеха; qn-m – вероятность наступления неудач. Формула Бернулли позволяет вычислять число успехов при многократном повторение опытов и широко применяется если мы хотим m испытаний. В ряде случаев на практике ставится задача интервальные оценки успехов р(а≤m≤b). Например, их число будет находиться в некотором интервале [а;b]. Тогда используется формула Муавра-Лапласа:
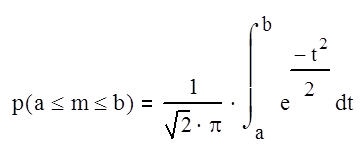
Здесь подынтегральная функция – функция Лапласа (которая относится к неберущимся интегралам и поэтому сведена в таблицу).
Формула Маувра-Лапласа
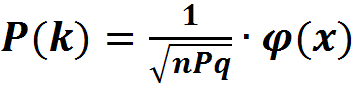
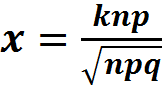
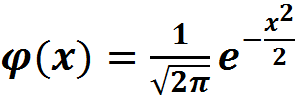
12 Дискретные и непрерывные случайные величины
Случайная величина (СВ) – такая величина, которая в результате некоторого опыта принимает то или иное значение, но какие именно – заранее не известно.
СВ является важным атрибутом отыскания случайных явлений, событий. Это особенно важно для отыскания состояния технических систем. СВ обозначаются латинскими буквами А, В, С,…, а их конкретные значения обозначаются маленькими буквами х1, х2, х3,…, хn. Тогда в этом случае некоторая с в конкретное случайное число с некоторой вероятностью:
р(Х=х1) = число
р(Х=хi) = 0
Рассмотрим несколько примеров:
1) Число пассажиров на платформе метрополитена ежедневно 8.00 утра определяется некоторым числом.
2) Число абонентов, соединенных АТС в течение каждого часа представляет некоторое число позвонивших или принявших звонок.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.