р(А) = 0,9 р(В) = 0,9 р(А) · р(В) = 0,81 Последовательное соединение ведет к произведению вероятностей и тем самым понижает надежность. Таким образом, последовательное соединение в реальной действительности не желательно.
Свойства случайных событий:
Cлучайные события также как и некоторые множества обладают некоторыми свойствами, знания которых позволяет определить состояние технических систем. 1) А + В = В + А – свойство коммутативности для сложения 2) А · В = В · А – свойство коммутативности для умножения (не верно для матриц) 3) А · (В · С) = (А · В) · С – свойство ассоциативности для умножения 4) (А + В) + С = А + (В + С) – свойство ассоциативности для сложения 5) А · (В + С) = АВ + АС – свойство дистрибутивности для сложения и умножения Доказываются также теоремы двойственности (де Моргана):
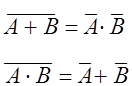
В ряде случаев используются продукционные правила событий
Если …, то … А→В
If …, then …
Если А влечет В, то АВ влечет А+В
![]() ,то
,то ![]()
То, что стоит после запятой называется следствие, реакция; после если – посылка.
1.8 О невозможности маловероятных событий
В реальной действительности и инженерной деятельности большое значение имеет обсуждение понятий: достоверное и невозможное события. Это обусловлено тем, что реальное положение вещей таково, что существуют события, которые теоретически нельзя отнести, например, к невозможным событиям. Вероятность их наступления так мала, с точки зрения инженера, они могут не произойти. Их можно отнести к различным классам, характеризующим их малую вероятность, а именно – к маловероятным событиям, практически невозможным событиям, или к почти невозможным событиям. Во всех этих случаях, с практической точки зрения эти события можно характеризовать как невозможные события. Так, например, событие с вероятностью 10-3 – 10-5 относятся к маловероятным событиям, а события 10-6 – 10-9 относятся к практически невозможным событиям. Так, например, событие, с вероятностью 1 шанс на 1000 и меньше, считаются малоосуществимыми в рамках однократного единичного опыта.
Таким образом, исключительно малые вероятности в технических системах позволяют при ближайшем рассмотрении отнести многие события, факты к практически невозможным событиям. Это позволяет не учитывать вероятность наступления этих событий.
6 Алгебра событий
2.1 общие соображения
Выше было показано, что события отличаются своим физическим смыслом, а также комбинациями и взаимодействием между собой. При этом возникает потребность выполнять некоторые операции с событиями (сложение, умножение, отрицание). Эти операции необходимы для численных расчетов, определяющих вероятность наступления, или ненаступления того, или иного события. Эти численные операции позволяют определять надёжность и риски технических и экономических систем. Для проведения таких расчетов используется алгебра событий, которая предполагает выполнение действий не с самими событиями, а с их вероятностями.
2.2 Теорема сложения для несовместных событий
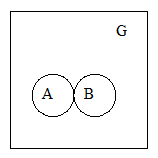 Теорема: вероятность появления одного из двух
несовместных событий (без различно какого) равна сумме вероятностей этих
событий.
Теорема: вероятность появления одного из двух
несовместных событий (без различно какого) равна сумме вероятностей этих
событий.
р(А + В) = р(А) + р(В) (*)
Доказательство: 1)Геометрическое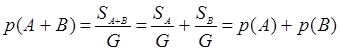
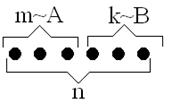 2)Аналитическое:
2)Аналитическое:
Пусть имеется несколько точек
р(А + В) = (m + k)/n = m/n + k/n = p(A) + p(B) Таким образом, сумма двух событий означает, что какое-либо из этих событий наступит. Этот случай распространяется на любое число событий. Теорема Колмогорова: вероятность появления одного из нескольких событий равна сумме вероятностей этих событий
p(А1 + А2 + А3 +…+An) = p(A1) + p(A2) +…+ p(An)
 р ΣAi =
Σ p(Ai)
р ΣAi =
Σ p(Ai)
пример: для противоположных событий:
р(А) + р(Ā) = 1, р(Ā) = 1 – р(А) = q(A)
Таким образом, с физической точки зрения, или прямое, или противоположное событие произойдет с вероятностью 1.
2.3 Теорема сложения для двух совместных событий
Теорема: вероятность появлеия хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.