Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 7

р(АВ) = р(В) · р(А/В), или р(АВ) = р(А) · р(В/А)

Свойства независимости и зависимости, таким образом легко установить при сравнении формул:

р(А) = р(А/В)

Иначе говоря, события независимые, когда безусловная вероятность равна условной вероятности, в противном случае события зависимые.

8 Общие, частные случаи зависимости и независимости событий

Выше было показано, что для независимых событий выполняется условие, что р(А) = р(А/В), р(В) = р(В/А) является условием независимости событий, иначе говоря, в этом случае условная вероятность равна безусловной, в противном случае р(А) ≠ р(А/В), или р(В) ≠ р(В/А) – события зависимые.

Условие зависимости и независимости тесно связано с задачей возвращения, или невозвращения шара:

1) В этом случае, событие А – вытаскивание белого шара, В – состоящее в вытаскивании второго шара становится независимым по отношению к событию А.

Так после возвращения шара, его вытаскивание не повлияло на вероятность второго шара.

2) В этом случае, после невозвращения первого шара, вероятность вытаскивания второго, очевидно, изменяется, тогда в этом случае, очевидно, события являются зависимыми, т.к. вероятность второго шара зависит от наступления первого.

Указанные теоремы обобщаются на любое число событий, например, для независимых событий, действует теорема Колмагорова:

р(А₁ + А₂ + А₃ + … + А_n) = p(A₁) + p(A₂) +…+ p(A_n)

Для зависимых событий необходимо использовать условную вероятность

р(АВС) = р(А) · р(В/А) · р(С/АВ)

Для любого числа событий будем иметь: = А₁(А₂/А₁) · А₂(А₃/А₂А₁) · … · А_n-1(A_n/A₁…A_n-1)

Условия зависимости и независимости событий позволяют уточнить формулу сложения для несовместных событий. р(А + В) = р(А) + р(В) – р(АВ) – для совместных событий

Тогда последний член в этом выражении зависит от того, являются ли события зависимыми, или независимыми.

Для независимых событий: р(А + В) = р(А) + р(В) – р(А) · р(В)

Для зависимых: р(А + В) = р(А) + р(В) – р(А) · р(В/А)

Т.к. из теоремы умножения следует, что р(АВ) для независимых событий равно произведению безусловных вероятностей, а для зависимых – произведение безусловной на условную вероятность.

Частные случаи

1) Зависимые и независимые события с достоверными, или невозможными событиями определяются следующими соотношениями: Любое событие Ас достоверным и невозможным событиями является независимым. р(А) = р(А/U); р(А) = р(А/V); р(А) = р(U/А); р(А) = р(V/А) Это обусловлено тем, что достоверное и невозможное события не зависят от того, произошло ли событие А, или не произошло. Равенства условной и безусловной вероятностей есть условие их независимости

2) Если А и Е независимы, то Ā и Е, Ē и А, Ā и Ē - тоже независимы

3) События могут быть независимы попарно: А и В, В и С, С и А – не зависимы

4) События могут быть независимы в совокупности: А₁, А₂, …, А_n – не зависят друг от друга Примечание: независимость в совокупности более сильное требование, чем попарная независимость.

2.9 Связь несовместных событий с зависимыми, или независимыми событиями

Не следует путать условия несовместности и совместности событий с их независимостью, или зависимостью.

В 1-м случае мы обсуждали вопрос: могут ли события наступить одновременно, или нет. Это условие определяется физическим смыслом задачи и здравым смыслом, но не математическим.

Во 2-м случае условие зависимости, или независимости определяется математическим выражением, но не физическим смыслом.

В этом случае совместное наступление событий р(АВ) имеет разные формулы, в зависимости зависят ли друг от друга события. Это есть математическое условие и требование зависимости и независимости событий.

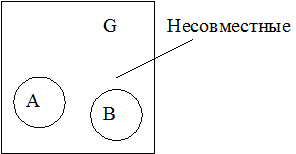Теорема: если события А и В несовместны и имеют некоторую вероятность наступления, то они обязательно зависимы.

Доказательство (от противного):

Для несовместных событий р(АВ) = 0, т.к. АВ – невозможное событие. Пусть, что события независимы, тогда : р(АВ) = р(А) · р(В) = 0. Условие выполняется, если либо р(А) = 0, либо р(В) = 0, либо р(А) и р(В) = 0. Однако, это противоречит условию, т.к. р(А)>0, p(B)>0. Значит события зависимы. Для совместных событий это условие соблюдается ограниченно: совместные события могут быть как зависимыми, так и независимыми.