Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 13

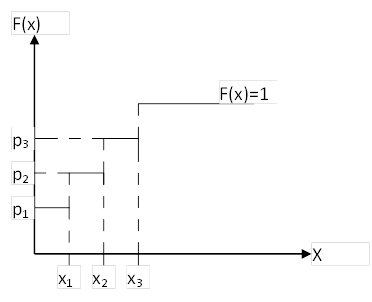
Примечание: вертикальные черточки у нас наносятся  в точках скачках вероятности.

Для НСВ: F(x) = p(X<x) + p[X=x_i]

Т.к. второй член этого выражения для НСВ равен 0 (p[X=x_i]=0), то функция распределения НСВ является частным случаем для ДСВ. В любом случае, функция распределения является возрастающей и накапливает вероятность для НСВ непрерывно, а для ДСВ – ступенчато.

Иначе говоря, функция распределения (F(x)) комулятивна (с накоплением) возрастает от 0 до 1.

Важные частные случаи

1) Если СВ (Х) принадлежит

интервалу (a , b), то функция распределения принадлежит этому интервалу

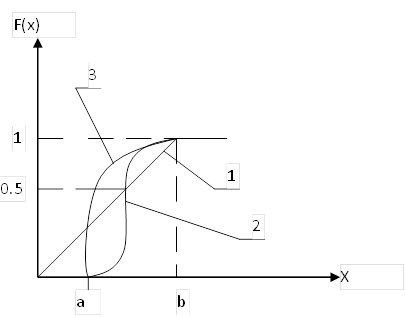
Здесь:

1- функция распределения для равномерного закона распределения

2- функция распределения для нормального закона распределения

3- функция распределения для экспоненциального закона распределения

2) Для НСВ, принадлежащей интервалу  граничные условия интервала не изменяют исходных положений.

p(a<X<b) = p(a≤X<b) = p(a≤X≤b) = p(a<X≤b)

Во всяком случае, т.к. граничные значения р(Х=а)=0 и р(Х=b)=0 границы интервалов, включающие, или невключающие их, как концов отрезка, но в интервал относятся к искусству автора. Т.к. функция распределения отражает свойства накопления вероятности (суммирование их), то функция распределения называется интегральным законом распределения

15  Плотность распределения СВ

Выше было рассмотрена функция распределения СВ, которая действительна как для НСВ, так и для ДСВ. Однако в ряде случаев, функция распределения – недостаточно удобный инструмент для определения вероятностей попадания СВ в некоторый интервал. В связи с этим вводится новое понятие – плотность распределения СВ.

Плотность распределения НСВ – это некоторая функция f(x), которая представляет собой первую производную от функции распределения. f(x) = F’(x)

Примечание1: Для того, чтобы найти плотность распределения f(x) функция распределения F(x) должна быть дифференцируема, поэтому плотность распределения может быть найдена только для НСВ.

Аналогом плотности распределения для ДСВ является многоугольник распределения.

Примечание2: Плотность распределения с физической точки зрения представляет собой скорость изменения, а точнее – скорость нарастания функции распределения.

Плотность распределения тем круче, чем круче изменяется функция распределения.

Плотность распределения в принципе характеризует СВ в некоторый интервал, пусть даже бесконечно малый.

Пусть СВ имеет некоторое приращение для своего конкретного значения.

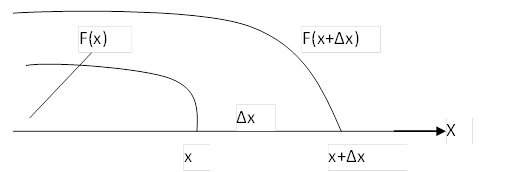
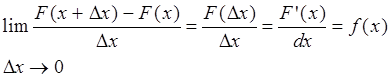Введем понятие элемент вероятности:

p(х <X< x+Δx) = p(x) ∙ Δx = S =Δp

Элементом вероятности называется некоторая площадь, ограниченная плотностью распределения и осью абсцисс на интервале (х ; х+Δx)

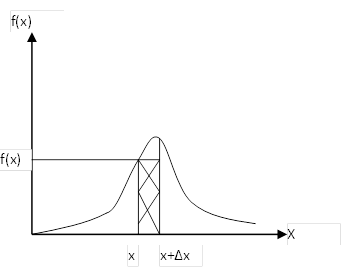
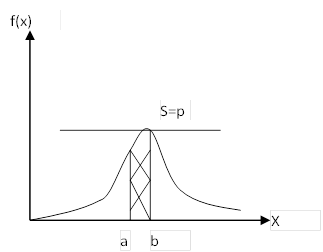
Приращение вероятности и сама вероятность попадания в заданный интервал (a,b)

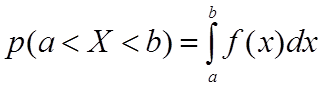
3.6 Свойства плотности распределения

1) Плотность распределения не отрицательная функция f(x)≥0, т.е. всегда находится выше оси абсцисс. Доказательство:

Т.к. F(x) – всегда возрастающая функция, то  ее производная всегда положительна.  2) Несобственный интеграл от плотности распределения в пределах от -∞ до ∞ равен 1.

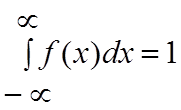
Доказательство:

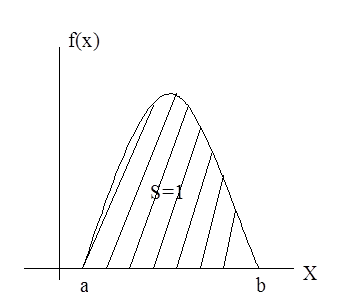
Вероятность попадания СВ в интервал от -∞ до ∞ есть достоверное событие с вероятностью р=1, в связи с этим площадь, ограниченна плотностью распределения и осью абсцисс равна 1.

3) Если СВ Х ограничена некоторым интервалом [а;b], то соответствующий интервал в этих пределах также равен 1.

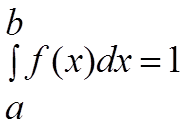
Доказательство:

Т.к. СВ Х с вероятностью 1 попадает в заданный интервал, то и площадь, ограниченна плотностью распределения, равна 1.

4) Если СВ распределена симметрично относительно 0, то и плотность распределения распределена симметрично относительно 0.

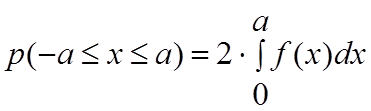
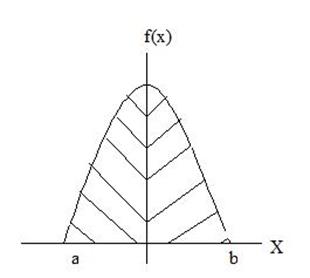
Определение функции распределения F(x) по известной плотности распределения f(x)