Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 11

13 Закон равномерного распределения ДСВ

Закон распределения ДСВ считается равномерным, если все значения этой СВ равновозможны и равновероятны.

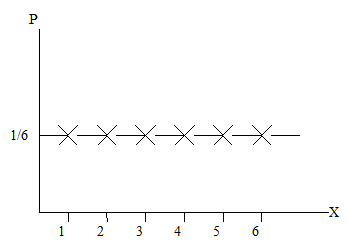p(X=xm) = 1/n

Примечание: линии, соединяющие точки многоугольника распределения не имеют физического смысла, а не наносятся из эстетических соображений.

Равномерный закон распределения (ЗР) для ДСВ для обывателя означает, что любое решение имеет равный шанс.

Равномерный ЗР в физическом смысле соответствует округлению значений на шкале приборов для некоторого обывателя.

II Закон геометрического распределения

ДСВ Х распределена по геометрическому ЗР, если вероятность случайных значений определяется выражением: p(X=x_m) = p∙q^m-1, m=1,2,3…n

Геометрическое распределение по своему физическому смыслу характеризует наступление некоторого успешного события после предыдущих неуспехов.

ПРИМЕР:

р(X=1) = p – если 1-ая попытка успешна (+)

р(X=2) = pq – если 1-ая неуспешная, а 2-ая попытка – успешная (-,+)

р(X=3) = pq² – (-,-,+)

Типичным примером геометрического распределения является запуск автомобильного двигателя, где в некоторых случаях успеху предшествует ряд неуспешных попыток.

ПРИМЕР: За время Т производится попытки включить двигатель автомобиля. Каждая попытка заканчивается успехом, с вероятностью 0,6 и занимает некоторое время τ. Определить ЗР до времени запуска двигателя и какова вероятность запустить двигатель через 4τ?

Считаем, что ЗР для СВ Х соответствует геометрическому распределению – геометрической прогрессии.

1,2,3,4 – число попыток

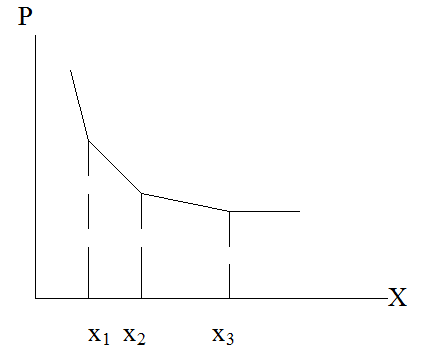Как видно, в геометрической прогрессии вероятность успеха катастрофически быстро убывает. Это характеризует тот факт, что, если первые попытки (1,2,3) означали неуспех, то четвертая – практически обречена.

Далее необходимо построить многоугольник распределения.

Геометрическое распределение в инженерной деятельности показывает, что необходимо повышать вероятность наступления события (успеха) первых двух-трех попыток.

III Биноминальный закон распределения ДСВ

ДСВ Х подчинена биноминальному ЗР, если она подчиняется следующему выражению:

Биноминальный ЗР вытекает из разложения бинома: (p+q)ⁿ

Биноминальное распределение, в принципе, тождественно формуле Бернулли и определяется ей.

С физической точки зрения, биноминальный закон также связан с испытаниями, когда часть испытаний (опытов) соответствует положительному результату (успех), а часть опытов соответствует отрицательным результатам (неуспех). Тогда в этом случае

++-+--+++---

p^m – характеризует число успехов

q^n-m – характеризует число неуспехов

Тогда по теореме умножения: p^m∙q^n-m – характеризует вероятность совместного наступления успехов и неуспехов, которые не могут произойти в одном единичном опыте одновременно.

Из этого количества выбирается некоторое число сочетаний (), которые определяют количество успехов в данной совокупности опытов. Биноминальный ЗР является достаточно сложным и в ряде случаев он может быть упрощён при принятии соответствующих гипотез.

IV Закон распределения Пуассона для ДСВ

На практике в сложных системах возникают обстоятельства, когда число n элементов достаточно велико, а вероятность наступления событий не так велика. В этом случае ЗР ДСВ определяется формулой Пуассона:

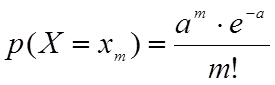, где а – некоторое a=n∙p=const

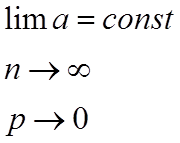
Закон Пуассона является приближенным отображением биноминального ЗР: 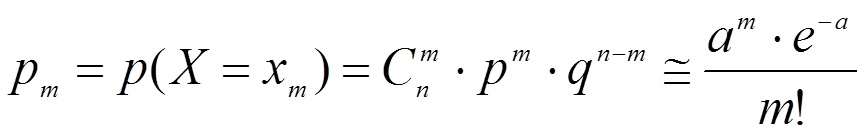, когда n→∞, а вероятность мала

Закон Пуассона играет большую роль и иногда называется законом редких событий, т.к. характеризует системы, в которых вероятность выхода из строя достаточно мала.

На первоначальном этапе Закон Пуассона нашёл хорошее физическое подтверждение в условиях таких физических испытаниях: