Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 2

1.2 Классическое определение вероятности

Прежде чем ввести это понятие договоримся об исходных постулатах. К ним относятся: 1) Все события будем обозначать большими латинскими буквами (А, В, С, D, X, Y). 2) Вероятность обозначается р (probability). 3)Величина противоположная вероятности q=1-p Вероятность – отношение числа опытов благоприятствующих событию А к числу всех опытов (это определение введено Лапласом и считается классическим), тогда р(А)=m/n, где р(А) – вероятность события А, m - число опытов благоприятствующих событию А, т.е. его наступлению, n – число всех опытов. Примечание: 1) Все опыты проводятся в одинаковых условиях; 2) результаты опытов являются равновозможными и несовместными.

Частные случаи:

1) Пусть все опыты благоприятствуют наступлению события А, тогда m=n, то р(А)=m/n=1.Тогда имеем дело с достоверным событием, которое обозначим U. Достоверное событие – такое, которое происходит всегда, наступает неотвратимо.

р(U)=1

Примеры: Восход солнца, предмет, брошенный вверх опускается вниз, никто не проживет 500 лет.

2) Пусть ни один из опытов не благоприятствует наступлению события А:m =0, то р(А)= 0/n=0. Такое событие называется невозможным (V).

р(V)=0

Невозможное событие – такое, которое никогда не происходит и не может произойти.  Примеры: нельзя изобразить число большее 1000 с помощью 3 чисел, вода не закипает при температуре 10 градусов и при нормальном давлении. На числовой оси указанные обстоятельства можно представить в следующем виде:

Отсюда следует, что строго говоря события V и U невозможны достоверно, не относятся к случайным, они либо всегда происходят, либо не происходят никогда. Поэтому их появление является строго или явление предсказуемым. Такие события или явления называются детерминистическими (детерминизм – строгая причинность). Из выше приведенных частных случаев следует, что

Т.е. вероятность равна или меньше единице и больше или равна 0. Отсюда следует, что классическое определение вероятности является исключительно простым и доступным, однако оно предполагает, что число благоприятных случаев известно заранее или легко подчитывается apriori (до опыта). Пример: в урне 6 белых и 4 черных шара. Какова вероятность вытащить белый шар? Ответ 0,6. Примечание: Все задачи в ТВ разделяются на два класса с возвращением шара, без возвращения шара.

1.3 Геометрическое понятие вероятности

Классическое понятие вероятности не всегда удобно, т.к. не распространяется на случаи с бесконечным числом опытов. В этом случае удобно применять геометрическое понятие вероятности.  Пусть задана некоторая плоскость G и некоторая совокупность элементарных исходов (событий) благоприятствующих событию А – g. Примечание: Элементарное событие – это некоторый неразложимый результат опыта ( в некоторых книгах простейшее событие). Геометрическая вероятность – событие состоящее в отношении площади g ко всей совокупности элементарных исходов G:

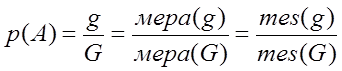
Иначе говоря: геометрическая вероятность – это отношение размеров. Они могут определяться 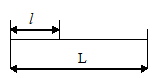отношением площадей, длин, или объемов.

р(А)=ℓ / L

Примеры:

1) Какова вероятность попадания наугад точки в круг вписанный в квадрат, если его радиус равен R?

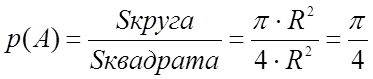
2) Какова вероятность попадание случайной точки в круг радиусом  R?

р(А)= 2/π

3) Задача о встрече. Две студента договорились о встрече между 12 и 13 часами, причем с условием что один из встречающихся ждет другого не более 20 минут.

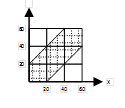
x-y≤20

р(А)=60²-40²/60²=5/9

Не смотря на довольно большое время ожидания вероятность встречи равна примерно 50%.

1.4 Статическое понятие вероятностей

В реальной действительности использование классического понятия вероятностей не всегда возможно, это обусловлено тем, что количество  благоприятных опытов не всегда известно (a’priori) до опыта. В связи с этим вводится новое, еще одно, понятие вероятностей, а именно – статистическая вероятность. Она определяется на основе некоторой статистики, как результат отношения опытов благоприятствующих событию А ко всем опытам, включающую данную статистику. Под статистикой понимается некоторый набор того или иного размера и его исход. Статистическое понятие вероятности является ключевым в инженерных дисциплинах. Т.к. именно оно позволяет оценить функционирование любых технических систем или технических устройств, а также риски связанные с их работой.