р(А + В) = р(А) + р(В) – р(АВ) (**)
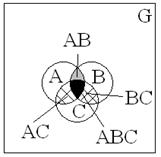Доказательство: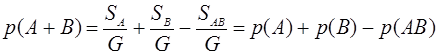 
Примечание: т.к. для несовместных событий АВ есть возможное событие, то р(АВ) = Ø, тогда выражение (*) становится частным случаем (**). Таким образом, формула сложения для несовместных событий является частным случаем формулы для совместных событий. Рассмотрим случай 3 совместных событий.
р(А + В + С) = р(А) + р(В) + р(С) – р(АВ) – р(АС) – р(ВС) + р(АВС)
В самом общем случае можно показать, что вычитаемое совместного события определяет необходимость добавления, или вычитания дополнительных членов уравнения.
7 Условная вероятность
Для совместных событий наступает новое понятие вероятности – условная вероятность. Это обусловлено тем, что т.к. события могут наступать совместно (одновременно) возникает влияние появления одного из событий на вероятность появления другого. Условная вероятность – вероятность р(А/В), которая характеризует меру того, что событие А произойдет при условии, что произошло событие В. Читается: вероятность наступления события А, при условии, что В произошло. Вероятность того, что студент закончил университет, при условии, что он закончил 2 курс.
Рассмотрим физическую сущность условной вероятности:
Пусть произведено n опытов, тогда из них m опытов благоприятствуют событию А, а также k опытов благоприятствует событию В. Т.к. события совместные, то есть также набор (часть) опытов, благоприятствующих как событию А, так и событию В. Тогда условная вероятность есть отношение числа опытов, благоприятствующих событию АВ к числу опытов, благоприятствующих событию В.
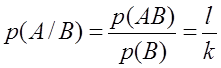
С физической точки зрения условная вероятность представляет собой отношение части исходов, благоприятствующих событию А, но выбранных из числа всех исходов, благоприятствующих событию В, отнесенные ко всем исходам, благоприятствующих событию В.
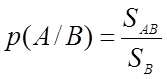
Пусть событие А состоит в том, что студент закончит 2 курс, а событие В – что студент, поступивший в универ, закончит его. Пусть р(А) = 0,9, т.к. одновременно заканчивает универ, одновременно заканчивает и 2 курс, то есть совместное наступление событий. р(В) = 0,85 Определить вероятность того, что студент, закончивший 2 курс, заканчивает и университет. р(В/А) = 0,85/0,9 = 0,94 Таким образом, вероятность окончания 3 курсов выше, чем окончание первых двух курсов. Условная вероятность играет важную роль, т.к. позволяет оценить как изменится вероятность наступления события, при условии, что некоторое другое, совместное с ним, известно (оно наступило).
2.5 Независимые и зависимые события
Наряду
с совместными и несовместными событиями существенную роль играют независимые и
зависимые события. Независимые события – событие, когда появление
одного из них не влияет на вероятность появления другого. В противном случае
события называются зависимыми. Пример:
при стрельбе из двух орудий показания одного из них может независеть от
попадания другого. Понятия независимости и зависимости являются взаимными. Так,
если А не зависит от В, то и В не зависит от А. Свойство независимости также
может быть попарным: если А не зависит от В, и В не зависит от С, то и А не
зависит от 
С. Свойства независимости могут
быть записаны для всей совокупности событий, когда событие А не зависит от всех
других событий, и все другие события также не зависят от А.
Свойства независимости и зависимости может определяться физическим смыслом задачи, однако существует и материальный критерий, определяемые теоремами умножения.
2.6 Теорема умножения для двух независимых событий
Вероятность совместного наступления двух независимых событий равна произведению вероятностей одного события на вероятность другого. р(АВ) = р(А) · р(В) Примечание: если это условие не соблюдается, то события зависимые.
2.7 Теорема умножения для двух зависимых событий
Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие произошло (вытекает из формулы условной вероятности).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.