Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 15

6) Если к СВ прибавить или отнять постоянную, то МО СВ будет равно ее МО ±const.

M[x±с]=M[x] ±с

7) Отклонение МО СВ от своего МО равно 0.

M[x-m_x]=0

С физической точки зрения «плюс/минус» отклонения уравновешивают друг друга по отношению к МО.

Доказательство:

M[x-m_x]=M[x]- m_x= M[x]- c=c-c=0

Таким образом, сумма отклонений не может характеризовать рассеивания, т.к. она всегда равна нулю. В ряде случаев используется центрирование СВ.

Операция центрирования:

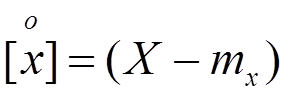
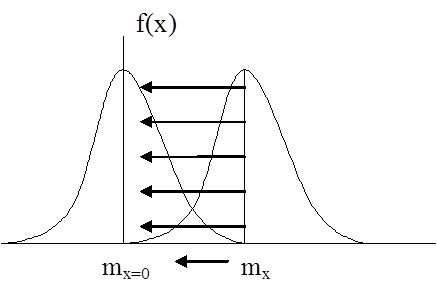
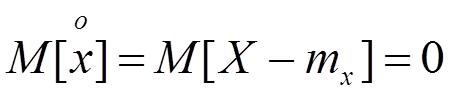
Операция центрирования позволяет привести СВ с разными МО к нулевому среднему и дальше их сравнивать, например, по величине рассеивания.

17 Дисперсия СВ

Наряду с характеристикой некоторого центра, относительно которого колеблется СВ необходимо ввести новую характеристику, которая собственно говоря и характеризовало сам факт рассеивания СВ и его величину.

Такой характеристикой является дисперсия, в точном переводе с латинского – рассеивание.

Дисперсия – это математическое ожидание (МО) квадрата отклонения СВ от её МО.

D_x = M [X - m_x]², или

Дисперсия определяется различным образом, как для ДСВ, так для и НСВ.

ДСВ: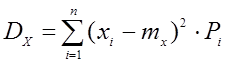

НСВ: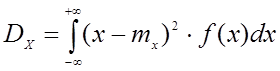

Недостатком дисперсии является то, что она измеряется квадратом физического параметра. Это неудобно в технических науках, в связи с этим на практике используется другая величина – среднеквадратическое отклонение (СКО). СКО равно положительному квадратному корню:

Размерность этой величины совпадает с размерностью МО и поэтому может суммироваться с ним. Например p(X = m_x ± 3σ_x) = 0.997

C физической точки зрения, дисперсия характеризует неопределенность СВ

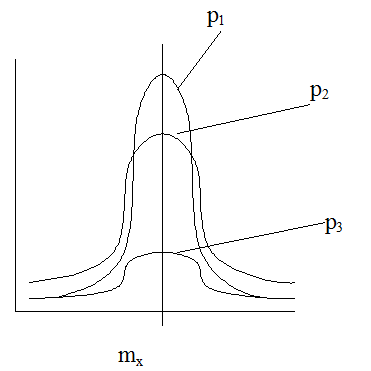
Площадь под всеми плотностями распределения равна 1

p₃ < p₂ < p₁

Очевидно, что, чем больше дисперсия, тем больше неопределенность

ПРИМЕР: Дисперсия биномиального закона распределения:

Dx = n ∙ p ∙ q

Mx = n ∙ p

3.11 Свойства дисперсии

1) Дисперсия постоянной величины равна 0:

D[c] = 0, где с=сonst

Это следует из физического смысла дисперсии, а также из ее свойства характеризовать рассеивание, которое в данном случае отсутствует.

2) Дисперсия всегда положительная величина:

D[c] > 0

Это вытекает из того обстоятельства, что квадрат как положительного, так и отрицательного числа является величиной положительной.

3) Константа (const) выносится за оператор дисперсии с возведением ее в квадрат:

D[c∙Х] = c² ∙ D[X]

Для СКО const выносится по абсолютной величине:

σ_x[c∙Х] = |c| ∙ σ_x

4) Дисперсия произведения двух случайных независимых величин равна произведению дисперсий этих величин:

D[X∙Y] = D[X] ∙ D[Y]

5) Дисперсия суммы, или разности двух случайных независимых величин равна сумме дисперсий этих величин:

D[X ± Y] = D[X] + D[Y]

Доказательство:

D[X ± Y] = D[X + D(-1)∙Y] = D[X] + (-1)² ∙ D[Y] = D[X] + D[Y]

Таким образом, дисперсия как суммы, так и разности СВ является суммой их дисперсий.

6) Дисперсия СВ + const равна дисперсии СВ (см. 1 свойство):

D[X + с] = D[X] + D[с] = D[X]

7) Дисперсию удобно вычислять по формуле, где она равна разности между математическим ожиданием квадрата СВ и квадратом ее МО (доказательство приведем далее):

D_х = M[x²] – m_x²

В реальной действительности дисперсия позволяет уточнить некоторый результат, получаемый детерминистическим путём (строгая причинность).

ПРИМЕР: ΔP = I²R

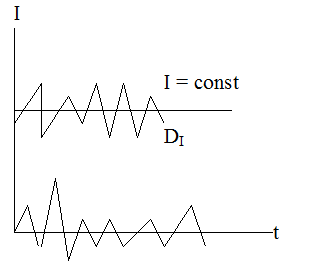
Однако, в реальной действительности ток имеет какую-то дисперсию, характеризующую ее отклонение, тогда потери: ΔP = I²R + D_IR

Статистические потери всегда выше детерминистических: ΔP_sto > ΔP_Dct

Коэффициент вариации

Большой интерес представляет отношение среднеквадратического отклонения СВ к её МО. Это отношение обычно выражается в процентах (%) и называется коэффициентом вариации:

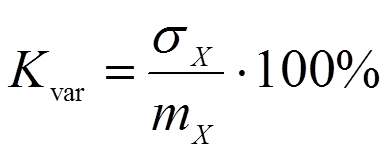
ПРИМЕР: В лотереи билет стоит 50$. В одной модели лотереи игрок может выиграть от 0 до 100$. σ_X = 100. В другой модели выигрыш может составить от 40 – 60$. В первом случае коэффициент вариации равен 100%, во втором – 50%. В какую игру играть зависит от склонности игрока к риску, который в данном случае характеризует коэффициент вариации.