Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 10

3) Число студентов получивших неуд в течение сессии на данном факультете.

Характерной чертой всех этих примеров является то обстоятельство, что все они имеют конкретное число изолированное друг от друга значений, которые являются целочисленными. Такие СВ называются дискретными (дсв).

ДСВ – называется величина, частное (возможное) значение которого можно пронумеровать, в этом случае мы имеем р(Х=х₁) = число

ДСВ наблюдается там, где значения СВ изолированы друг от друга и каждое из них может быть обозначено числом.

Рассмотрим примеры:

1) Абсцисса отклонения снаряда из некоторого орудия по отношению к прямому направлению (боковое уклонение).

2) Отклонение точки попадания снаряда по дальности.

3) Отклонение амплитуды синусоидального напряжения в отдельной квартире.

Характерной чертой всех этих примеров является то обстоятельство, что СВ заполняют весь интервал свободных значений.

Значения СВ примыкают друг к другу и неотделимы между собой, такие с в называются непрерывными (НСВ).

Так как число точек в некотором интервале бесконечно, то вероятность попадания СВ в некоторую точку равную 0. Иначе говоря НСВ примет какое-то конкретное значение х_i на непрерывной оси равной 0.

р(Х=х_i) = 0

Тогда бессмысленно искать вероятность того, что некоторая СВ примет конкретное значение, ибо эта вероятность для НСВ равна 0.

В связи с этим в этих случаях необходимо искать вероятность попадания СВ в некоторый интервал пусти как угодно малый. В этом коренное отличие НСВ от ДСВ.

Аксиоматическое определение СВ - СВ Х, связанная с данным опытом есть числовое функция, определяемая на множестве достоверных событий.

Это говорит о том, что СВ определяется из некоторой области G, которая представляет собой множество достоверных событий.

В реальной действительности многие НСВ (аналоговые сигналы) определяются с помощью приборов через некоторый интервал времени.

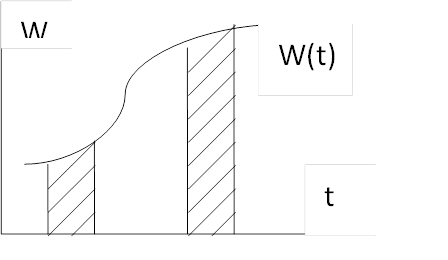
Непрерывный процесс измеряется в моменты времени t₁ t₂ и t₃ t₄, тогда интервал между этими временами называется уровнем квантования. Чем меньше интервал квантования, тем более точно оцифровывается НСВ и таким образом НСВ → ДСВ.

Реальные СВ разбиваются на два больших класса: ДСВ и НСВ, для которых законы распределения, формулы определения числовых характеристик, оценки рисков определяются различными формулами. В связи с этим отношение той или иной СВ к одному из классов должно быть начальной первостепенной задачей.

3.2 Понятие закона распределения ДСВ

Закон распределения ДСВ – соответствие, установившее связь между возможными значениями СВ и соответственными их вероятностями.

p_m = p(X=x_m), где m = 1,2,3…n

Различают следующие формы представления закона распределения ДСВ:

1) Ряд распределения – некоторая таблица соответствующая значениям СВ и соответствующими им вероятностями. Т.к. все возможные значения СВ (Х) представляют собой полную группу событий, то для любого ряда распределения сумма вероятностей равна 1.

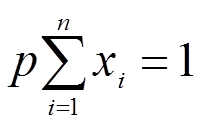
Требуется определить, какое число имеет максимальную вероятность и какова сама вероятность?

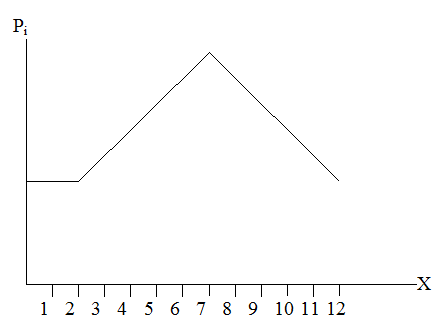2) Многоугольник распределения – ряд распределения может быть представлен в графической форме, по оси абсцисс откладываются значения СВ, а по оси ординат – их вероятность.

Многоугольник распределения представляет собой координаты некоторых точек и инцидентные (инциденция – совпадение) некоторому x_i и их вероятности.

3) Аналитическая форма закона распределения – форма закона, которая может быть представлена некоторым аналитическим выражением.

В этом случае вероятность конкретного значения (x_i ) СВ (X) определяется некоторой формой: p(X=x_i) = p∙q^i-1

В этом выражении р – вероятность наступления события СВ; q – вероятность ненаступления

Выбор той, или иной формы закона распределения ДСВ определяется исследователем, как правило, для небольших статистических выборах можно ограничиться рядом распределения. При больших статистических данных удаётся установить некоторое аналитическое выражение для ДСВ.