Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 3

р(А)^*= m/n

р(А)^* - статистическая вероятность, m - число опытов, благоприятствующих событию А, n - число всех опытов. В отличие от классического понятия вероятностей р(А)^* существенно зависит от числа опытов, при этом при числе опытов стремящихся к бесконечности статистическая вероятность стремится к своему истинному классическому значению.

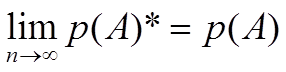
Как видно с увеличением числа опытов р(А)^* стремится к классической вероятности

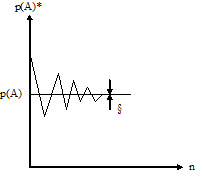
Графически это можно представить:

При конечном числе опытов статическая вероятность все меньше отклоняется от классической вероятности и в итоге ошибка или неточность определения определяется некоторой разностью между этими вероятностями, равной «§ (кси)».  Очевидно, что чем больше опытов, тем более достоверной является оценка вероятностей. Отсюда вытекают пожелания иметь как можно большую статистику (набор данных) для получения достоверного значения вероятности.  Таким образом, мы имеем три понятия вероятностей: классическое, геометрическое и статистическое. Применение каждого из них определяется условием задачи и относится к искусству автора.

3 Вероятность и комбинаторика

В обыденной жизни существуют некоторые построения, обстоятельства или задачи выбора того или иного выигрыша или другого решения, когда приходится иметь дело с комбинациями тех или иных элементов или цифр. В частности – вероятностные игры, но не только. В этом случае некоторому решению ставится в соответствие некоторая комбинация чисел или иных элементов. Раздел математики занимающийся комбинациями называется комбинаторикой. Различают 3 вида комбинаций:

 1) Перестановка – комбинации, отличающиеся перестановкой элементов. Предполагается что элементы меняются местам, но число элементов n – не меняется. P_n=n!

Доказательство: 1) n=1, 1! = 1 2) А и В, n=2, АВ и ВА, 2! = 1∙2 = 2 3) А, В, С, n=3, АВС, ВСА, СВА, АСВ, САВ, ВАС, 3! = 1∙2∙3= 6 Для n=4 число перестановок равно 24 Для n=5 число перестановок равно 120

Примечание: Число перестановок в общем случае можно искать:n=n(n-1)!    0!=1

2) Сочетание – комбинации из n элементов по m, отличающиеся содержанием.

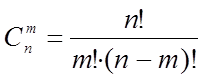
Мы не интересуемся порядком элементов, а только их содержанием.

3) Размещение – комбинация n по m, отличающаяся не только содержанием, но и порядком элемента.

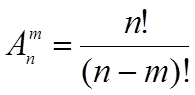
ПРИМЕР: азбука Морзе, флажки на кораблях. Размещений больше чем сочетаний на величину перестановок m элементов.

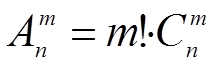
Если размещения допускают повторения, то

Дополнительные правила комбинаторики:

1) Правило суммы: Если из некоторой совокупности объектов, объект А может быть выбран n способами, а объект В – m способами, то либо А либо В могут быть выбраны (n+m) способами. 2) Правило умножения: Если из некоторой совокупности объектов, объект А может быть выбран n способами, а после этого объект В – m способами, то пара этих объектов (в таком же порядке) может быть выбрана (n*m) способами.

4  Классификация и соотношение случайных событий

Случайные события являются результатом (следствием) некоторого опыта, эксперимента. При этом во многих случаях удобно оперировать с понятием элементарного события, которое рассматривается как неразложимый результат опыта. Классификацию событий удобно рассматривать с помощью диаграмм Венна. В этом случае события рассматриваются на плоскости в некотором пространстве. 1) Пусть задано некоторое исходное пространство всех элементарных событий с исходами G = {g1, g2, g3, … , gn}. При этом часть опытов благоприятствует некоторому событию А (элементарных событий g1, g2 …). A ~ m. p(A) = A/G – геометрическая вероятность

Это есть исходный постулат для диаграмм Венна.

2) Суммой двух событий А и В является событие, входящее либо в А, либо в В, либо в А и В одновременно. А + В = А U B (объединение)

Примечание: объединение двух событий соответствует логической связке «или».

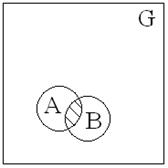3) Произведение двух событий А и В называется событие, состоящее из области, в которую входит событие А и В одновременно.