Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 16

18 Квантили СВ

Диапазон, в котором встречается СВ может быть разбит на некоторый интервал, который в свою очередь характеризует вероятность того, что СВ попадет в этот интервал.

Квантили СВ называется вероятность того, что СВ с функцией распределения F(x) примет значение q:

F(x) = p(X < x_q) = q

ПРИМЕР:

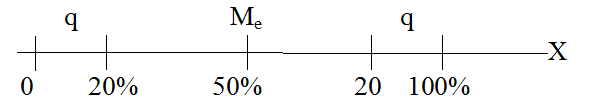
p=q

Квантиль с уровнем q=20% - число бедных, тогда q=100% и выше характеризует число богатых и сверхбогатых.

Квантиль q=0.5 соответствует медиане

Квантили q=0.25 (25%) называются квартили

Квантили q=0.1 (10%) называются децили

Интервалы квантилей позволяют наглядно определить процент явлений, процессов, СВ, или случайных событий, попадающих в тот, или иной диапазон интервала, доступного СВ.

Коэффициент вариации

Большой интерес представляет отношение среднеквадратического отклонения СВ к её МО. Это отношение обычно выражается в процентах (%) и называется коэффициентом вариации:

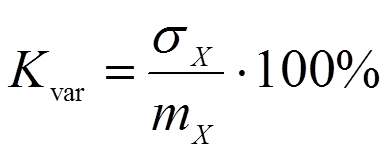
ПРИМЕР: В лотереи билет стоит 50$. В одной модели лотереи игрок может выиграть от 0 до 100$. σ_X = 100. В другой модели выигрыш может составить от 40 – 60$. В первом случае коэффициент вариации равен 100%, во втором – 50%. В какую игру играть зависит от склонности игрока к риску, который в данном случае характеризует коэффициент вариации.

19 Моменты высших порядков

Выше были рассмотрены две характеристики СВ, а именно МО и дисперсия, однако этих двух характеристик недостаточно, чтобы полностью заменить закон распределения СВ.

Поэтому определяются дополнительные числовые характеристики, частным случаем которых являются и первые две.

Эти характеристики по аналогии с механикой называются моментами высших порядков. Различают 2 группы: моменты начальных порядков и моменты центральных порядков.

1) Начальным моментом k-го порядка называется МО СВ в k-ой степени:

α = M[X^k]

Для ДСВ: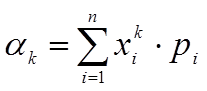

Для НСВ: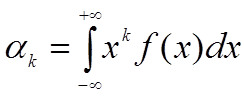

По своему физическому смыслу начальные моменты характеризуют в более тонкой степени центрированное значение СВ, её среднее положение.

k=0: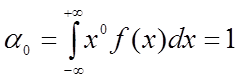

k=1: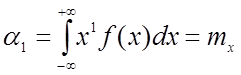

Таким образом начальный момент 1-го порядка равен МО, а выражения: МО и начальный момент 1-го порядка являются синонимами.

k=2: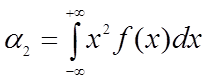

Начальный момент 2-го порядка характеризует отклонение МО от больших СВ.

2) Центральным моментом k-го порядка называется МО разности СВ и её МО в k-ой степени

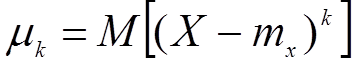
ДСВ: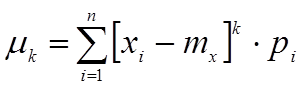

НСВ: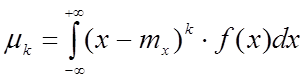

k=1:

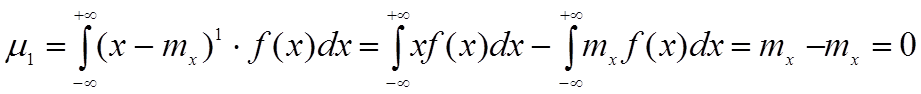
Этим доказывается 7-ое свойство МО.

k=2:

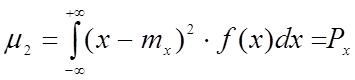
Дисперсия – это второй центральный момент

Центральные моменты могут выражаться через начальные моменты, так для дисперсии имеем:

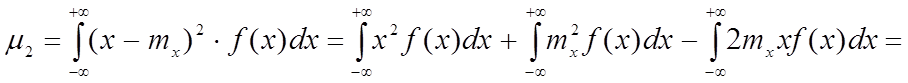
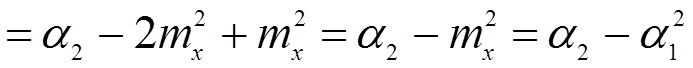
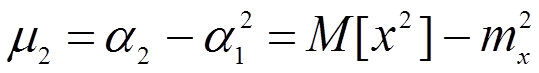
Этим доказывается 7-ое свойство дисперсии.

k=3:

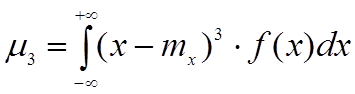
Третий момент центрального порядка характеризует асимметрию ЗР. Численно асимметрия выражается коэффициентом асимметрии:

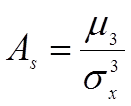
Деление на  необходимо для того, чтобы сделать коэффициент асимметрии безразмерной величиной, т.к. μ₃ имеет размерность [м³].

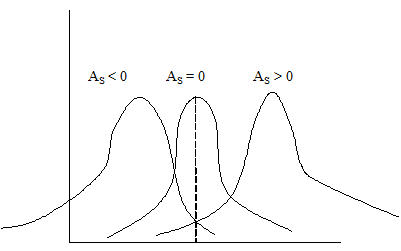
1) Если ЗР – симметричный, то, очевидно, A_S = 0

2) Если правый хвост распределения более длинный (скособоченность направо), то коэффициент A_S > 0

3) Если левый хвост распределения более длинный (скособоченность налево), то коэффициент A_S < 0

Очевидно, что асимметричность ЗР СВ является дополнительной характеристикой к МО и дисперсии.

k=4:

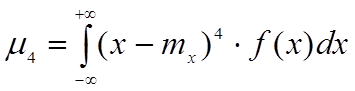
Характеризует островершинность, или уплощенность ЗР СВ; численной характеристикой является эксцесс

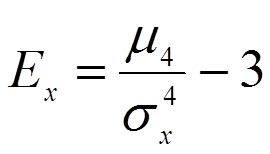
Деление на  делает эксцесс безразмерным, а минус 3 – вычетается искусственно, чтобы сделать эксцесс равным 0 для нормального ЗР

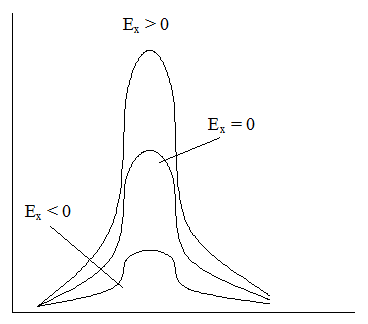
1) Если ЗР – нормальный, то E_x = 0 ) Если ЗР – более островершинный, то E_x > 0 3) Если ЗР – более плоский, то E_x < 0 Моменты более высших порядков физического смысла не имеют и рассматриваться нами не будут. ПРИМЕЧАНИЕ: Центральные моменты для симметричных ЗР: μ1 = 0, μ2 = 0, μ3 = 0. Это значит, что все нечетные моменты для симметричных ЗР всегда равны 0