Определенность и неопределенность научного познания. Алгебра событий. Классификация и соотношение случайных событий, страница 8

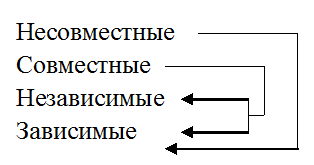
С точки зрения физического смысла несовместные события всегда зависимы, т.к. если не произойдет 1-ое событие, то 2-ое обязательно произойдет

9 Вероятность появления хотя бы одного события

На практике часто возникают случаи, когда нужно определить вероятность того, что произойдет некоторое событие хотя бы один раз. Это условие определяется следующей теоремой:

Теорема: вероятность появления хотя бы одного из событий А₁, А₂, …, А_n, независимых в совокупности, равна разности между 1 и произведением вероятностей противоположных событий.

p(А) = 1 – q₁ ∙ q₂ ∙…∙ q_n, где q₁ = 1 – p(A₁) = p(Ā₁); q₂ = 1 – p(A₂) = p(Ā₂); … q_n = 1 – p(A_n) = p(Ā_n)

Здесь q – вероятность того, что событие не произойдет.

В частном случае, когда вероятность наступления событий одинакова, формула имеет следующий вид:  р(А) = 1 – qⁿ

 n – число событий в совокупности

Пример1: Вероятность события А, состоящего в том, что студент сдаст экзамен р(А) = 0,4, т.к. он знает только 40% материала. Сколько раз он должен сдавать экзамен, чтобы с вероятностью большей, или равной 0,9 он сдал бы экзамен хотя бы один раз.

Дано:

р(А) = 0,4

р(А) ≥ 0,9

n - ?

Будем полагать, что при n опытах экзамен будет сдан, а также события являются независимыми в совокупности и имеют равную вероятность: р(А) = 0,4 => q(A) = 1 – 0,4 = 0,6

p(A) = 1 – 0,6ⁿ ≥0.9 => 0.6ⁿ ≤ 0.1 =>

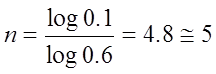
Т.к. допустимо сдавать экзамен не более 3 раз, то полученный результат свидетельствует о возможности исключения.

Пример2: Пусть событие А состоит в том, что студент обязательно сдаст экзамен из 3-х испытаний (n=3). При этом р(А) = 0,936. Какова вероятность, что студент сдаст экзамен в одной попытке, т.е. появится 1 раз в одном испытании.

Дано:

p(A) = 0.936

n = 3

p(A) - ?

Решение:

0,936 = 1 – q³ => q³ = 0,064 => q = 0.4 => р(А) = 0,6

Таким образом, вероятность сдать экзамен в одном испытании равна 60%. Иначе говоря, вероятность 0,6 сдачи экзамена в одном испытании является предельной, для того, чтобы сдать его в 3-х испытаниях.

Следует всегда иметь ввиду, что, когда требуется найти вероятность появления хотя бы одного события из некоторой совокупности А₁, А₂, …, А_n всегда проще найти вероятность противоположных событий Ā₁, Ā₂, …, Ā_n и затем вычесть их произведение из единицы:

р(А₁ + А₂ +…+ А_n) = 1 – р(Ā₁)∙ р(Ā₂)∙…∙р(Ā_n)

Аналогичным образом, может быть определена условная вероятность некоторого события через условную вероятность противоположного события:

р(А/Е) = 1 – р(Ā/Ē)

Указанные формулы являются изящным решением для совместных, или несовместных событий, при этом появление одного из событий означает появление его в одном испытании.

10 Формула полной вероятности

В реальной действительности наступление какого-либо события связано часто с наступлением других событий, что делает их связь через условную вероятность. При этом другие события также могут быть случайными. Их следует рассматривать как некоторые гипотезы. Пусть имеется некоторая совокупность событий, составляющих полную группу, которые влияют на наступление события А. Назовем их гипотезами: Н₁ + Н₂ + … + H_n = U

Т.к. гипотезы составляют полную группу событий, то, что произойдет одно из них, является достоверным событием. Представим также, что гипотезы являются несовместными, тогда:

H_i ∙ H_j = V

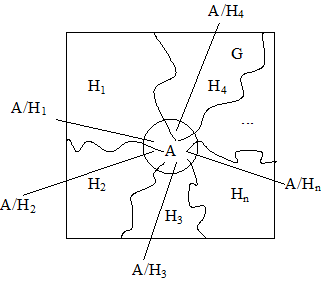
Тогда на диаграмме Венна указанные условия будут иметь следующий вид:

Видно, что событие А может реализоваться (наступить) с одной из гипотез Н₁, Н₂, …, H_n. Пусть также известны a’priori вероятности наступления этих событий: р(Н₁), р(Н₂), …, р(H_n), тогда событие А происходит одновременно с одной из гипотез:

А = AU = A(Н₁ + Н₂ + … + H_n)

p(A) = p(AН₁) + p(AН₂) + … + p(AH_n)

Таким образом эта формула соответствует теореме сложения для совместных событий A и H_i. Наряду с этим можно применить теорему умножения, тогда вероятность появления события А, которое может произойти лишь при условии появления одного из нескольких случайных несовместных событий H_i – гипотез равна сумме произведений вероятностей этих гипотез на условную вероятность появления события А, при условии, что данная гипотеза состоялась: