Во времена кавалерийских войск всегда наблюдались случаи гибели кавалеристов от удара копытом их лошадей. Попытка подсчитать вероятность гибели солдата от удара копытом подтвердили хорошее совпадение этой вероятности Закону Пуассона. И это понятно, т.к. число кавалеристов n велико, а число смертей от лошади является редким событием и, таким образом, проверка показала совпадение экспериментальных данных с теорией, а также то, что Закон Пуассона необходимо применять для редких событий.
В технических системах закону Пуассона подтверждается время наработки на отказ. Первый отказ в любой технической системе является СВ.
14 Функция распределения СВ
Во многих случаях мы имеем дело не только с ДСВ, но и с непрерывными, поэтому законы распределения ДСВ не являются универсальным средством для решения вероятностных задач. В связи с этим вводится новое понятие – функция распределения СВ, которая является универсальной, как для дискретной, так и для непрерывных СВ.
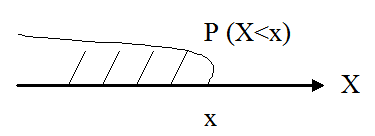Функция распределения СВ Х определяет вероятность того, что СВ Х примет значение
меньшее, чем на перёд заданное значение х: F(x) = p(X<x)
С физической точки зрения это означает вероятность того, что СВ «Х» не превзойдёт некоторого на перёд заданного значения «х», иначе говоря, что на оси абсцисс все значения СВ будут находиться левее некоторого на перёд заданного значения.
3.4 Свойства функции распределения
1)
Функция распределения находится в интервале (0;1). 
. Это
свойство вытекает из того, что функция распределения есть вероятность, а
вероятность изменяется от 0 до +1. С физической точки зрения очевидно, что,
если х→-∞, то F(x)=0. И, если х→+∞, то F(x)=1.
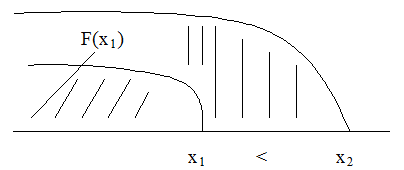
Эти условия вытекают из того, что в первом случае событие становится невозможным, а во втором случае – оно становится достоверным. 2) Функция распределения F(x) является возрастающей функцией, при этом для НСВ это монотонно возрастающая функция, а для ДСВ – ступенчато возрастающая. F(x2)>F(x1), если х2>х1
Это обусловлено тем, что вероятность попадания в интервал (х2 ; -∞) больше, чем вероятность попадания в интервал (х1 ; -∞).
3) Вероятность попадания СВ (Х) в интервал (a ; b) равна разности функции распределения на этом интервале
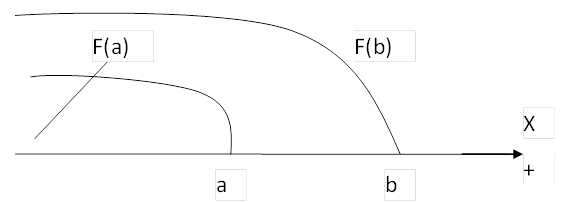
р(a ≤ X < b) = F(b) – F(a), b>a
F(b) = F(a) + р(a ≤ X < b)
Т.к.
вероятность величина положительная, то отсюда следует, что F(b)>F(a),
что подтверждает предыдущее свойство, что F(x) –
возрастающая функция. В общем случае, вероятность того, что 
будет равно:
Если b>a и «b» устремить в «а» (b→a), то F(b) – F(a) = 0. Это означает, что р(Х=а) = 0
С физической точки зрения, это означает, что вероятность того, что непрерывная СВ (Х) примет некоторое конкретное значение равна 0, и, таким образом, определение вероятности конкретному значению НСВ бессмысленно. Получается парадоксальное явление! Ранее мы считали, что вероятность может быть равна 0 только для невозможного события. Однако в данном случае событие возможно, и более того, это событие обязательно произойдёт для одной из точек; однако, для каждой из точек в отдельности вероятность его наступления равна 0, а потому его следует считать практически невозможным. Это явление называется парадоксом вероятности и обусловлено тем, что вероятность конкретного значения НСВ (Х=а) практически невозможно и равна 0. Практически возможное событие, но с ничтожно малой вероятностью принимается за невозможное событие р(А) = 0
Это означает, что невозможное событие всегда имеет вероятность равную 0, однако вероятность равная 0 в полной мере не означает, что событие невозможно. А как же быть с теоремой суммы вероятностей событий? Можем ли мы здесь складывать эти вероятности? Недоумение можно рассеять тем, что теорема сложения вероятностей оперирует со счётным множеством, но не с бесконечным числом множеств. По аналогии с тем, что площадь фигуры определяется суммой некоторого числа, пусть бесконечно малых площадей, но не точек, ибо площадь любой точки равна 0. А сколько нулей не складывай, то получится 0. Тогда также получается парадокс: складывая 0 получим нулевую площадь, что абсурдно! В связи с этим необходимо искать вероятность попадания СВ в некоторый интервал, пусть как угодно малый. Выше были рассмотрены условия определения вероятности для НСВ, тогда F(x) монотонно возрастающая функция. Для ДСВ функция распределения имеет разрывы, т.к. вероятность накапливается скачкообразно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.