Целью структурного анализа механизма является определение количества звеньев и кинематических пар, классификация последних, определение подвижности пар и степени подвижности механизма, а также выделение в нем структурных групп – кинематических цепей, у которых число входов совпадает с числом степеней подвижности.
1) Звенья механизма: 1 – кривошип; 2 – звено AKD; AK-кулиса; 3 – камень кулисы; 4 – шатун DE; 5 – ползун E.
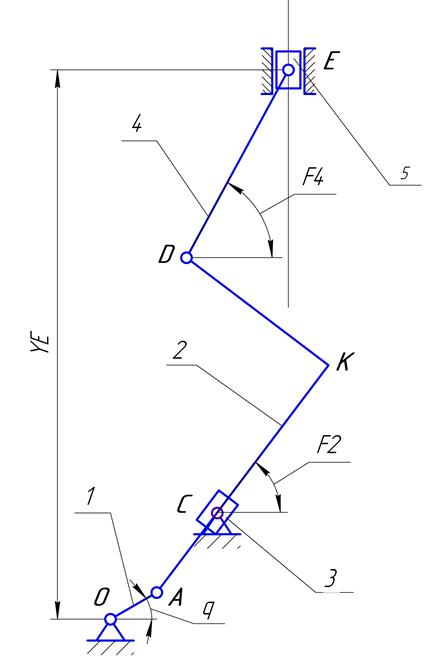
Рис.1.1. Схема механизма
2) n = 1 (один вход О-А).
3) Граф механизма:
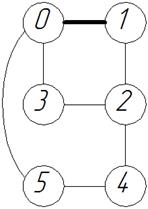
Рис.1.2. Граф механизма
4) Число подвижных звеньев механизма N = 5; количество кинематических пар совпадает с числом подвижностей пар P = S = 7.
5) K = P – N = 2, т.е. два независимых контура.
6) Число степеней подвижности по формуле Чебышева W = 3N – 2pн – pв = 3.5 – 2.7 = 1
7) W = n, то есть рассматривается нормальный механизм.
8) В плоскости движения нет избыточных связей и лишних подвижностей.
9) Разделение графа механизма на подграфы, соответствующие структурным группам.
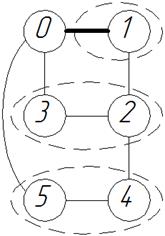
Рис.1.3. Структурный граф механизма
10) Структурный граф механизма
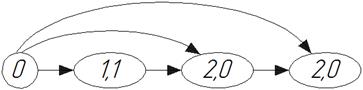
Рис.1.4. Структурный граф механизма
Механизм образован следующим образом: к стойке присоединяется однозвенная одноподвижная группа (звено 1) и две двухзвенные группы Ассура – ВПВ (звенья 2 и 3) и ВВП (звенья 4 и 5).
Целью геометрического анализа рычажного механизма является составление уравнений геометрического анализа, решение их, выделение побочных и основных решений, определяющих положения звеньев, а также исследование функций положения выходных звеньев структурных групп.
1) Уравнения геометрического анализа.
Здесь и далее все неизвестные, которые необходимо определить из данной системы или из данного уравнения подчёркнуты.
Функции положения для группы I (кривошип OA):
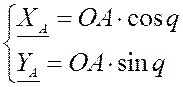
Групповые уравнение для группы II (ВПВ):
![]()
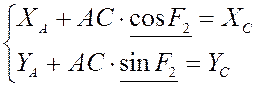
Функции положения точки K:
![]()
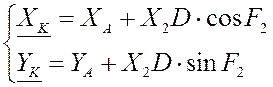
Функции положения точки D:
![]()
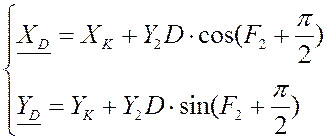
Групповые уравнение для группы III (ВВП):
![]()
![]()
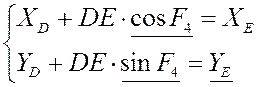
2) Решение уравнений геометрического анализа в общем виде
а) Группа ВПВ:
Перенесём все неизвестные части влево, а известные – вправо:
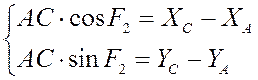
Возведём обе части в квадрат:
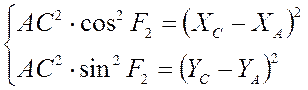
Сложим два уравнения:
![]()
![]()
Отсюда легко можно найти ![]() и
и ![]() :
:
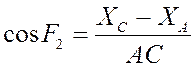
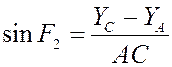
И следовательно, мы можем найти и
сам угол ![]() .
.
б) Группа ВВП:
Напомним, что:
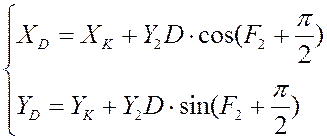
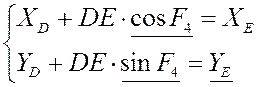
Отсюда мы можем определить ![]() :
:
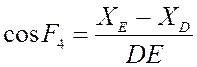
Тогда:
![]()
Здесь ![]() , то есть существуют два решения уравнения.
Этим решениям соответствуют два варианта сборки звеньев группы ВВП. На рис.2.4
один из них, соответствующий основному решению (-), показан сплошными линиями,
а другой, соответствующий побочному решению (+), изображен пунктирными линиями.
, то есть существуют два решения уравнения.
Этим решениям соответствуют два варианта сборки звеньев группы ВВП. На рис.2.4
один из них, соответствующий основному решению (-), показан сплошными линиями,
а другой, соответствующий побочному решению (+), изображен пунктирными линиями.
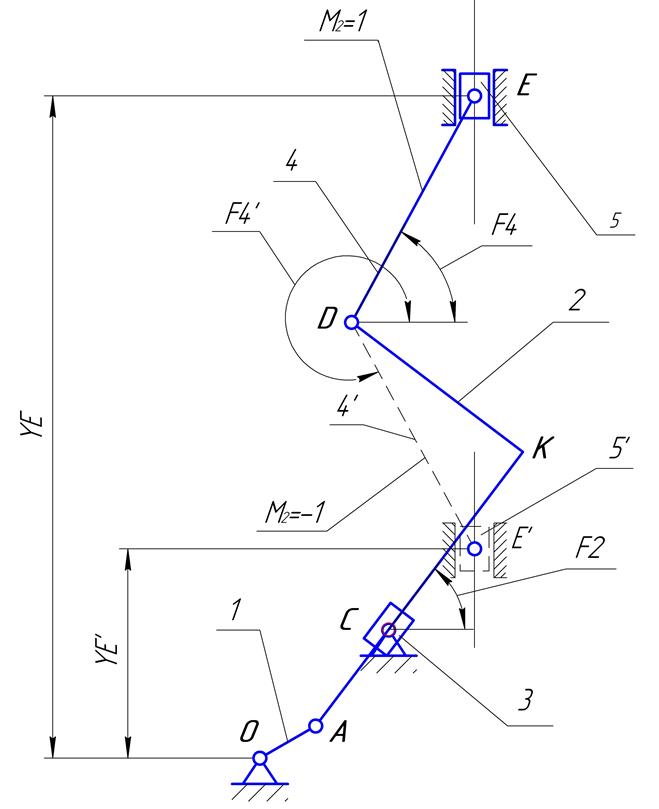
Рис.2.3. Две сборки механизма
Положение
группы типа ВВП, при котором обход шарниров в последовательности E, D, K
происходит против часовой стрелки, соответствует способу сборки ![]() , если же обход идёт по часовой стрелки,
как в случае с E′DK,
то способ сборки
, если же обход идёт по часовой стрелки,
как в случае с E′DK,
то способ сборки ![]() .
.
В
исходной схеме ![]() .
.
Далее найдём ![]() :
:
![]()
Все расчёты представлены в приложении в протоколе MathCad.
Из неравенства
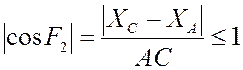 можно получить условие существования
группы ВПВ:
можно получить условие существования
группы ВПВ:
![]() , где
, где ![]()
Из неравенства
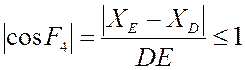 несложно получить
условие существования группы ВВП:
несложно получить
условие существования группы ВВП:
![]()
Масштаб 1:10 см
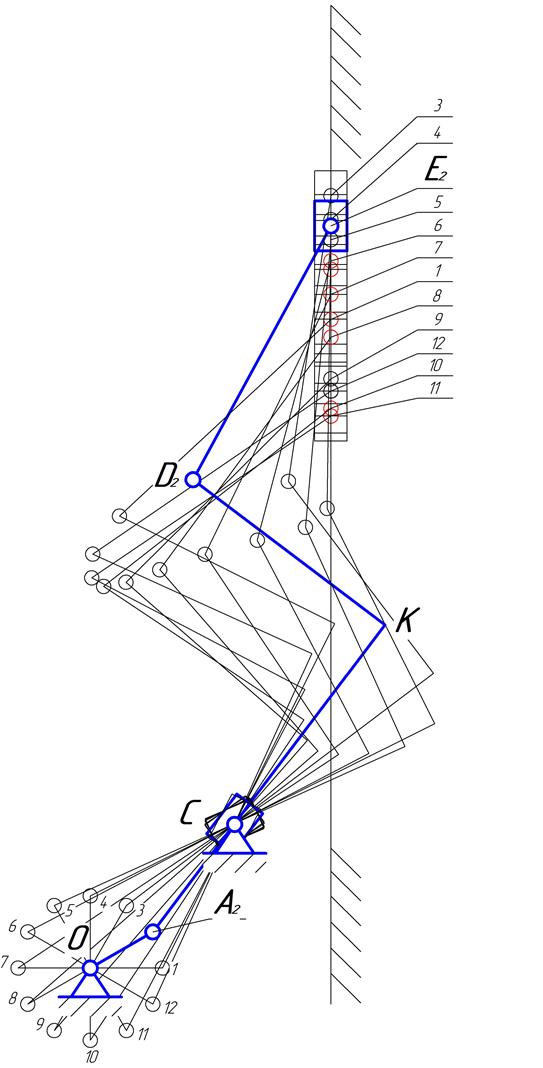
Рис. 2.4. 12 положений механизма
1) Дифференцируя уравнения геометрического анализа для группы I (кривошипа) по q, мы получаем аналог скорости точки A:
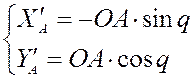
Дифференцируя уравнения второй раз, мы получаем аналог ускорения точки A:
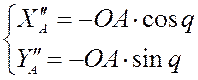
2) Дифференцируя первое уравнение геометрического анализа для группы ВПВ по q, мы получаем следующее:
![]()
Напомним выражение для AC:
![]()
Тогда 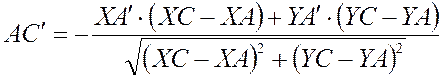 .
.
Сразу же определим ![]() :
:
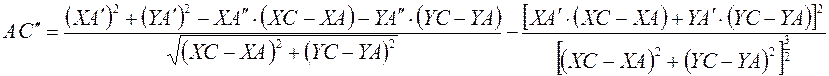
Отсюда мы можем найти аналог
угловой скорости ![]() :
:
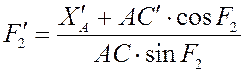
Приведём к более удобному для второго дифференцирования виду:
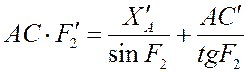
Дифференцируя уравнение второй раз, мы получаем следующее:
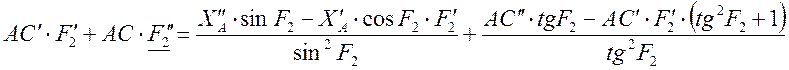
Отсюда мы можем найти аналог
углового ускорения ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.