Дифференцируя уравнения геометрического анализа для группы ВВП2 по q, мы получаем следующее:
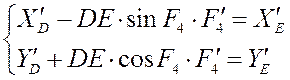
Отсюда мы можем найти аналог
угловой скорости шатуна DE ![]() и аналог скорости ползуна E
и аналог скорости ползуна E ![]() :
:
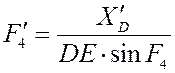
![]()
Дифференцируя уравнения второй раз, мы получаем следующее:
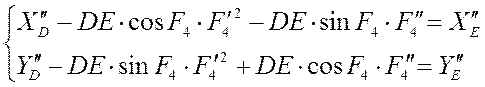
Отсюда мы можем найти аналог
углового ускорения шатуна DE ![]() и аналог ускорения ползуна E
и аналог ускорения ползуна E ![]() :
:
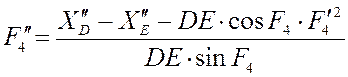
![]()
Якобианом системы уравнений группы ВВП2 будет являться определитель следующей матрицы:
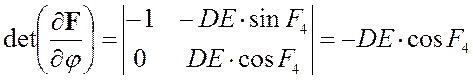
Здесь 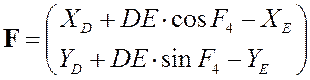 , а
, а 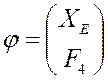 .
.
Когда якобиан обращается в ноль, мы получаем:
![]()
Следовательно,
якобиан обращается в ноль при 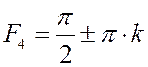 ,
, ![]() . Это означает, что якобиан обращается в
ноль в тех положениях, при которых шатун DE расположен параллельно
вертикальной прямой, по которой ходит ползун E.
Это – особое (сингулярное) положение группы BBП2.
В действительности же этого не происходит, так как не выполняется условие
существования группы ВВП2:
. Это означает, что якобиан обращается в
ноль в тех положениях, при которых шатун DE расположен параллельно
вертикальной прямой, по которой ходит ползун E.
Это – особое (сингулярное) положение группы BBП2.
В действительности же этого не происходит, так как не выполняется условие
существования группы ВВП2:
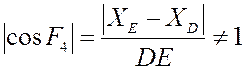
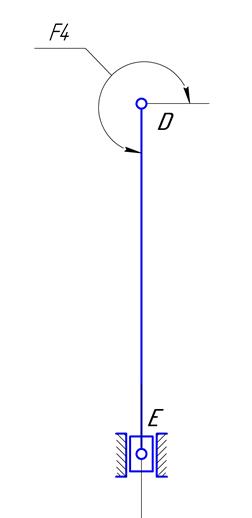
Рис.3.2. Особое положение группы ВВП2
Все расчёты представлены в приложении в протоколе MathCad.
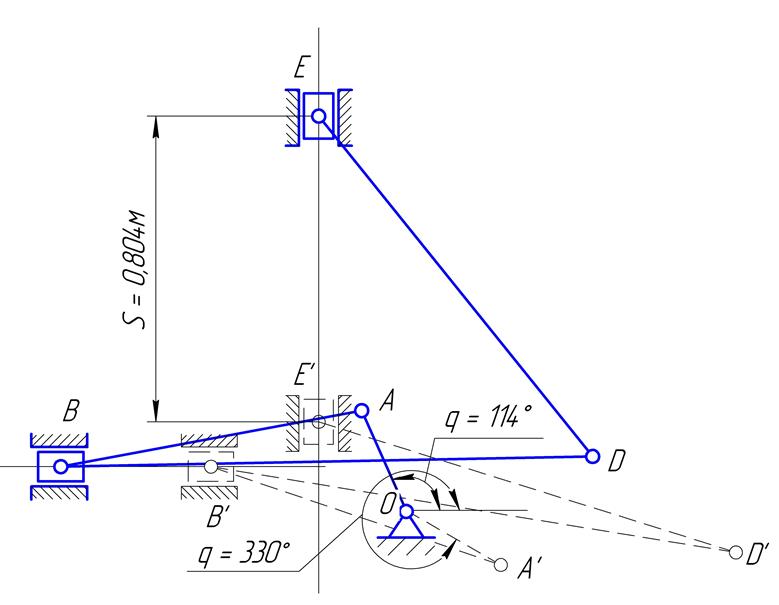
Рис.3.1. Механизм в крайних положениях
1) а)
План аналогов скоростей при ![]() .
.
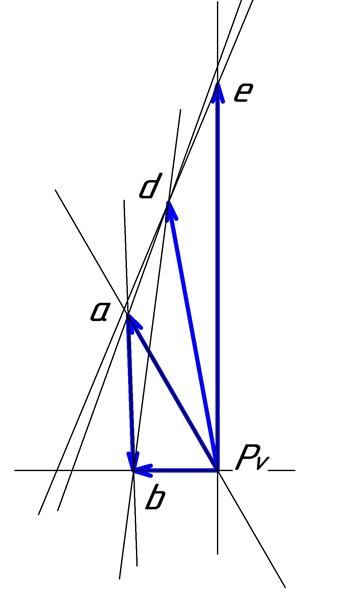
Рис.3.2.
План аналогов скоростей при ![]()
Для построения плана аналогов скоростей выберем полюс ![]() и масштаб:
и масштаб:
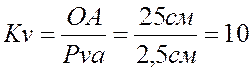
Уравнение для группы ВВП1:
![]()
Аналог угловой скорости звена ABD и ![]() определяется
выражением:
определяется
выражением:
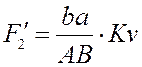
Уравнение для группы ВВП2:
![]()
Аналог угловой скорости ![]() определяется выражением:
определяется выражением:
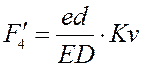
б) План аналогов ускорений при ![]() .
.
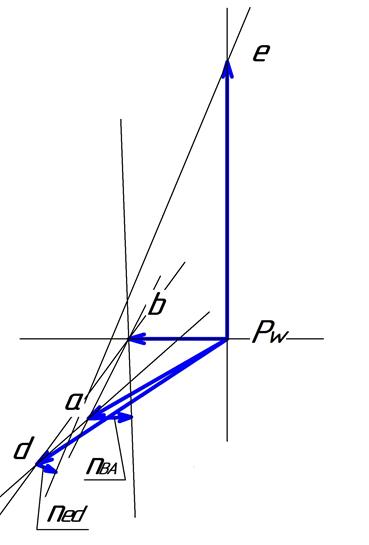
Рис.3.5.
План аналогов ускорений при ![]()
Для построения плана аналогов ускорений
выберем полюс ![]() и
масштаб:
и
масштаб:
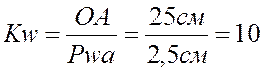
Уравнения для группы ВВВ:
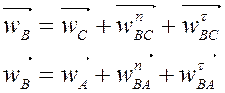
Точка C неподвижна 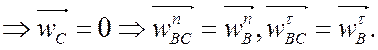
Тогда:
![]()
Аналог нормальной составляющей ускорения точки B относительно точки A определяется выражением:
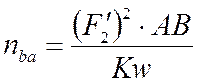
Аналог углового ускорения звена ABD ![]() определяется
выражением:
определяется
выражением:
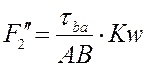
Уравнение для группы ВВП2:
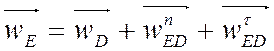
Аналог нормальной составляющей ускорения точки E относительно точки D определяется выражением:
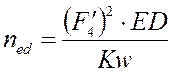
Аналог углового ускорения шатуна ED ![]() определяется
выражением:
определяется
выражением:
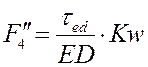
Направление аналогов угловых скоростей и ускорений показано на рис.3.6.
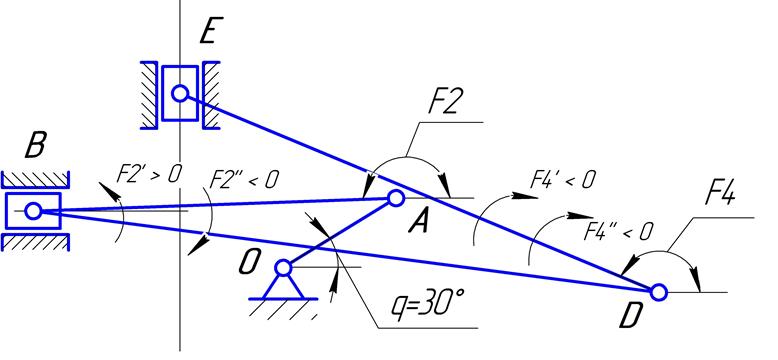
Рис.3.6. Направление
аналогов скоростей и ускорений при ![]()
Расчёт по представленным выше формулам с учётом знаков (все линейные размеры в метрах):
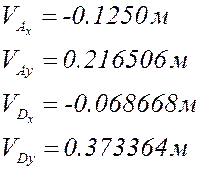
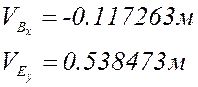
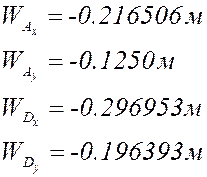
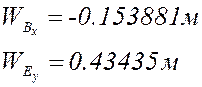
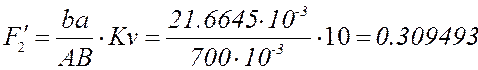
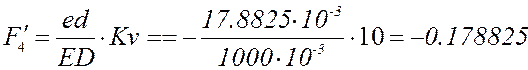
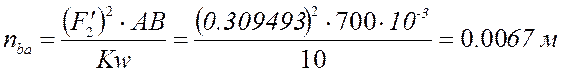
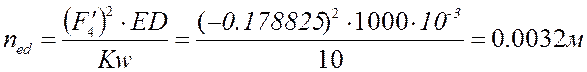
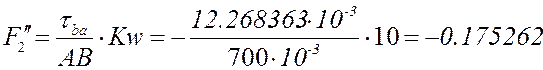
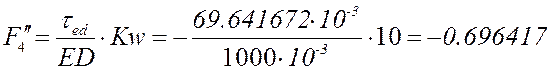
План аналогов скоростей и
ускорений в крайнем положении при ![]() представлен в приложении
2.
представлен в приложении
2.
Расчёт для ![]()
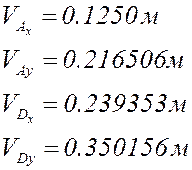
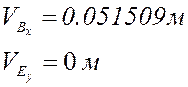
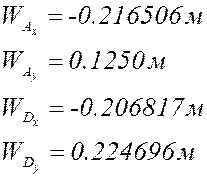
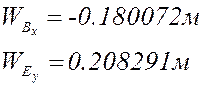
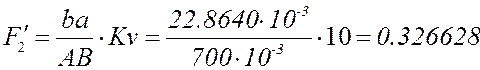
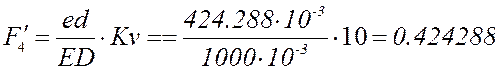
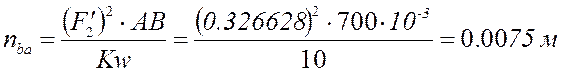
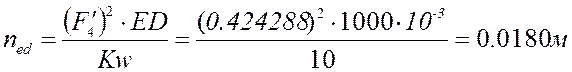
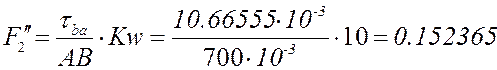
|
График функции положения точки Е. |
|
График аналогов скорости и ускорения точки Е. |
|
|
|
|
|
|
При ![]() .
.
|
Графический метод |
Стандартная программа |
Протокол |
|
|
XA |
0.216506 |
0.216506 |
0.216506 |
|
YA |
0.125000 |
0.125000 |
0.125000 |
|
X'A |
-0.125000 |
-0.125000 |
-0.125000 |
|
Y'A |
0.216506 |
0.216506 |
0.216506 |
|
X"A |
-0.216506 |
-0.216506 |
-0.216506 |
|
Y"A |
-0.125000 |
-0.125000 |
-0.125000 |
|
XB |
-0.483047 |
-0.483047 |
-0.483047 |
|
YB |
0.100000 |
0.100000 |
0.100000 |
|
X'B |
-0.117263 |
-0.117263 |
-0.117263 |
|
Y'B |
0.000000 |
0.000000 |
0.000000 |
|
X"B |
-0.153881 |
-0.153881 |
-0.153881 |
|
Y"B |
0.000000 |
0.000000 |
0.000000 |
|
XD |
0.72333 |
0.72333 |
0.72333 |
|
YD |
-0.057015 |
-0.057015 |
-0.057015 |
|
X'D |
-0.068668 |
-0.068668 |
-0.068668 |
|
Y'D |
0.373364 |
0.373364 |
0.373364 |
|
X"D |
-0.296953 |
-0.296953 |
-0.296953 |
|
Y"D |
-0.196393 |
-0.196393 |
-0.196393 |
|
XE |
-0.200000 |
-0.200000 |
-0.200000 |
|
YE |
0.326992 |
0.326992 |
0.326992 |
|
X'E |
0.000000 |
0.000000 |
0.000000 |
|
Y'E |
0.538473 |
0.538473 |
0.538473 |
|
X"E |
0.000000 |
0.000000 |
0.000000 |
|
Y"E |
0.43435 |
0.43435 |
0.43435 |
|
F2 |
-177.9533° |
-3.105871 (-177.95328°) |
-3.105871 |
|
F'2 |
0.309492 |
0.309492 |
0.309492 |
|
F"2 |
-0.175262 |
-0.175262 |
-0.175262 |
|
F4 |
157.4179° |
2.747461 (157.4179°) |
2.747461 |
|
F'4 |
-0.178819 |
-0.178819 |
-0.178819 |
|
F"4 |
-0.696416 |
-0.696416 |
-0.696416 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.