Кинематический и силовой анализ рычажных механизмов, страница 2

2.  Геометрический анализ механизма

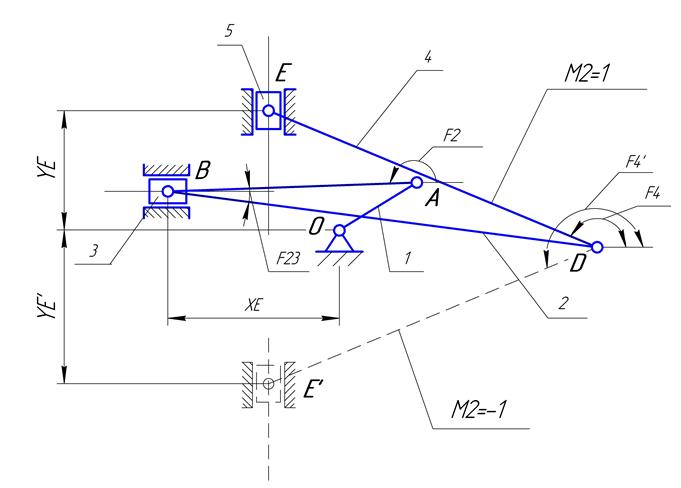
Целью геометрического анализа рычажного механизма является составление уравнений геометрического анализа, решение их, выделение побочных и основных решений, определяющих положения звеньев, а также исследование функций положения выходных звеньев структурных групп.

2.1.  Групповые уравнения и их решение

1)  Уравнения геометрического анализа.

Здесь и далее все неизвестные, которые необходимо определить из данной системы или из данного уравнения подчёркнуты.

Функции положения для группы I (кривошип OA):

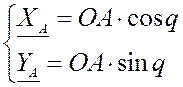
Групповые уравнение для группы II (ВВП₁):

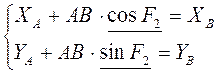
Функции положения точки D:

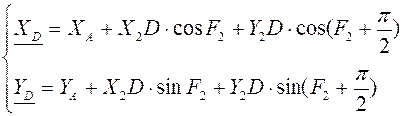
Уравнение для определения F3 - угла поворота BD:

                                      

Групповые уравнение для группы III (ВВП₂):

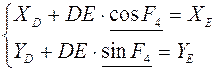
Решение уравнений геометрического анализа представлено в приложении 1.

2)  Решение уравнений геометрического анализа в общем виде

а) Группа ВВП₁:

Перенесём все неизвестные части влево, а известные – вправо:

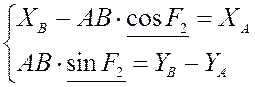
Выразим из нижнего уравнения , а затем по основному тригонометрическому тождеству  :

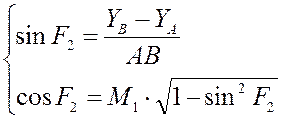
Здесь , то есть существуют два решения уравнения. Этим решениям соответствуют два варианта сборки звеньев группы ВВП₁. На рис.2.1 один из них, соответствующий основному решению (-), показан сплошными линиями, а другой, соответствующий побочному решению (+), изображен пунктирными линиями.

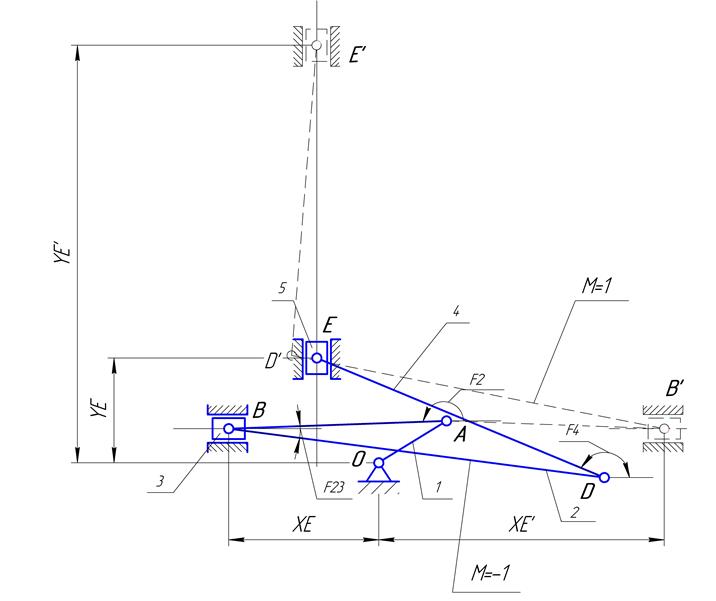
Рис.2.1. Две сборки механизма

Положение группы типа ВВП₁, при котором обход шарниров в последовательности A, B, D происходит по часовой стрелки, соответствует способу сборки , если же обход идёт против часовой стрелки, как в случае с AB′D’, то способ сборки . В исходной схеме .

б) Группа ВВП:

Напомним, что:

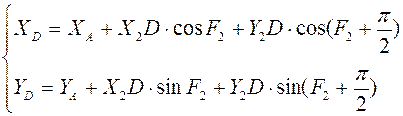
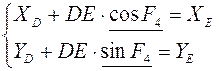
Отсюда мы можем определить :

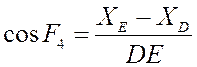
Тогда:

Здесь , то есть существуют два решения уравнения. Этим решениям соответствуют два варианта сборки звеньев группы ВВП₂. На рис.2.2 один из них, соответствующий основному решению (+), показан сплошными линиями, а другой, соответствующий побочному решению (-), изображен пунктирными линиями.

Рис.2.2. Две сборки механизма

Положение группы  ВВП₂, при котором обход шарниров в последовательности A, D, E происходит против часовой стрелки, соответствует способу сборки , если же обход идёт по часовой стрелки, как в случае с ADE′, то способ сборки .

В исходной схеме .

Далее найдём :

Все расчёты представлены в приложении в протоколе MathCad.

Из неравенства 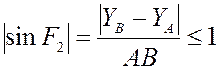 можно получить условие существования группы ВВП₁:

Из неравенства 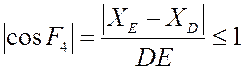  несложно получить условие существования группы ВВП₂:

2.2.  План 12 положений механизма

Масштаб 1:10 см

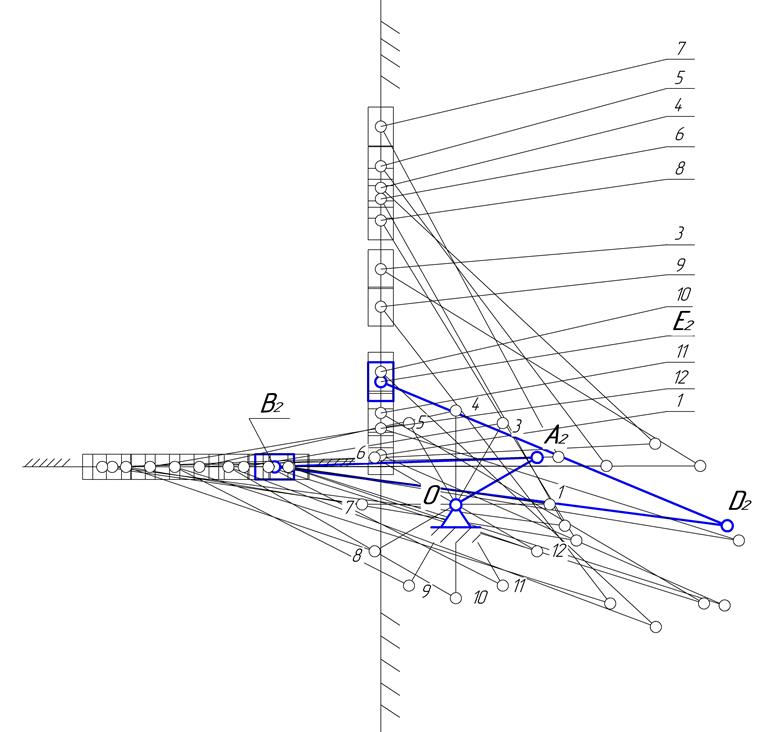
Рис.2.3. План 12 положений механизма

3.  Кинематический анализ механизма

3.1.  Аналитическое определение аналогов скоростей и ускорений

1)  Дифференцируя уравнения геометрического анализа для группы I (кривошипа) по q, мы получаем аналог скорости точки A:

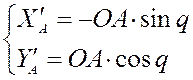
Дифференцируя уравнения второй раз, мы получаем аналог ускорения точки A:

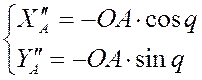
2)  Дифференцируя уравнения геометрического анализа для группы ВВП₁ по q, мы получаем следующее:

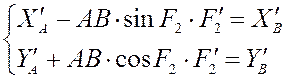
Отсюда мы можем найти аналог угловой скорости звена АВD   и аналог скорости ползуна В :

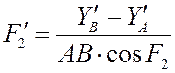
Дифференцируя уравнения второй раз, мы получаем следующее:

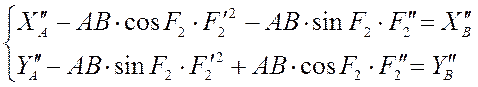
Отсюда мы можем найти аналог углового ускорения звена АВD   и аналог ускорения ползуна В :

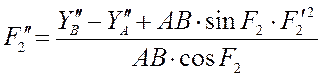
Якобианом системы уравнений группы ВВП₁ будет являться определитель следующей матрицы:

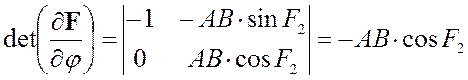
Здесь 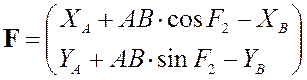, а .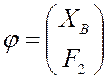

Когда якобиан обращается в ноль, мы получаем:

Следовательно, якобиан обращается в ноль при 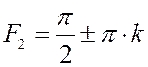, . Это означает, что якобиан обращается в ноль в тех положениях, при которых шатун AB расположен перпендикулярно горизонтальной прямой, по которой ходит ползун B. Это – особое (сингулярное) положение группы BBП₁. В действительности же этого не происходит, так как не выполняется условие существования группы ВВП₁:

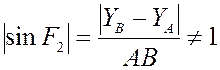
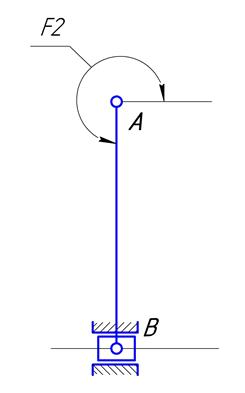
Рис.3.1. Особое положение группы ВВП₁

3)  Дифференцируя уравнения функции положения точки D по q, мы получаем аналог скорости точки D:

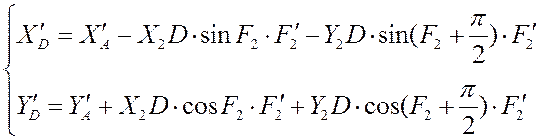
Дифференцируя уравнения второй раз, мы получаем аналог ускорения точки D:

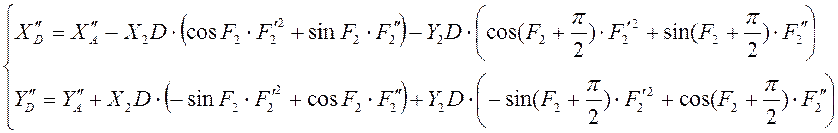
4)  Группа ВВП₂: