Диагностика электрооборудования электрической железной дороги (по опыту Горьковской железной дороги), страница 17

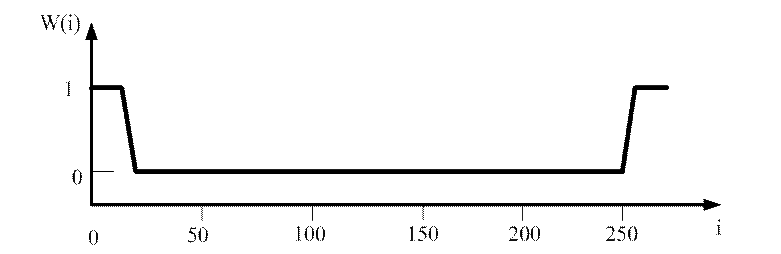
Рисунок 3.3 – Спектр, очищенный от шума

 Полезно обратить внимание на два момента. Поскольку спектр после прямого БПФ симметричен относительно центра спектрограммы, то фильтрация должна быть также симметричной. Второй момент – применённая фильтрация равносильна заданию так называемого прямоугольного окна. Она неплохо показывает себя при простых сигналах – в выделенном сигнале (рисунок  3.4) почти не осталось и намека на шум.

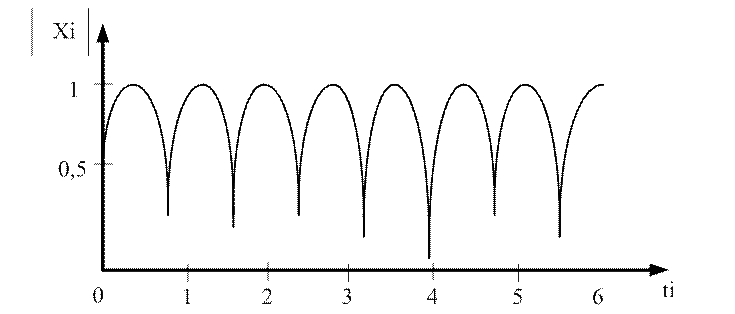
Рисунок 3.4 – Сигнал, очищенный от шума

 Однако при более сложных сигналах, особенно импульсных, такое ограничение спектра приводит к колебательным процессам на временной зависимости сигналов, известным как эффект Гиббса. Именно поэтому форму окна желательно выбирать иной – без резкого ограничения частотной области.  

Спектр для несинусоидальной функции в виде ряда прямоугольных импульсов продолжительностью  с высотой , при начале отсчета времени, сдвинутом на  представлен, на рисунке 3.5.

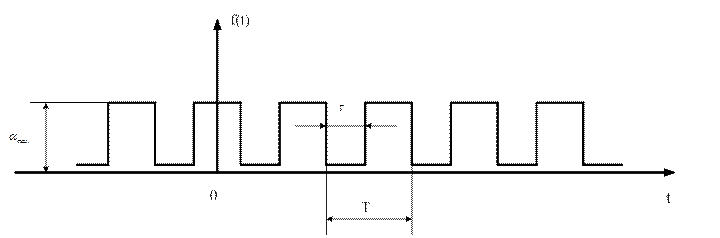
Рисунок 3.5 – Спектр для несинусоидальной функции

Эта функция симметрична относительно оси ординат, и её разложение в тригонометрический ряд имеет вид:

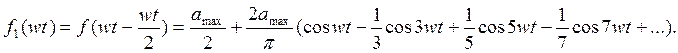 (3.1)

Спектры амплитуд и фаз этой функции показаны на рисунке 3.6. Естественно, что спектр амплитуд остался прежним.

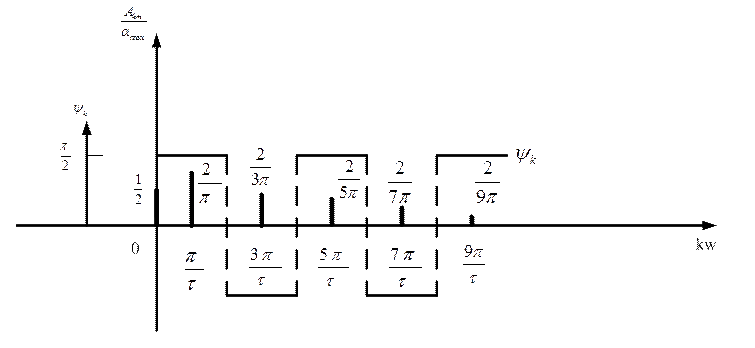
Рисунок 3.6 – Спектр амплитуд и фаз

Рассматривая каждую гармонику как сумму членов ряда для  и переходя от записи

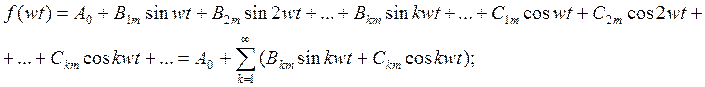       (3.2)

к

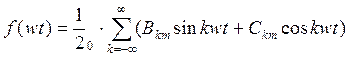;                                                  (3.3) 

можно этому выражению придать следующий вид:

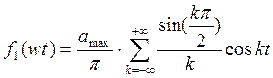;                                                                 (3.4)

Действительно, при k=0

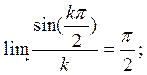                                                                                     (3.5)   

т.е. получаем постоянную составляющую; при четных значениях k члены ряда обращаются в нуль, а при k нечетных 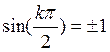  и при суммировании членов для положительных и отрицательных k дают амплитуду, равную   .

Спектр амплитуд в этом случае имеет симметричный вид (рисунок 3.7).

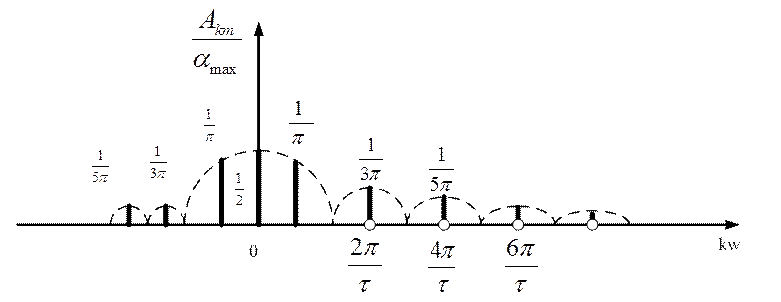
Рисунок 3.7 – Симметричный спектр амплитуд

Такое рассмотрение гармонических составляющих как совокупности колебаний положительных и отрицательных частот во многих случаях позволяет получить более простое общее выражение. Отрицательная частота, конечно, не имеет физического смысла, и составляющие ряда при   являются не чем иным, как удобным математическим выражением гармоник, имеющих положительную частоту, соответствующую модулю k.      

4 Экспериментальное исследование системы вибродиагностики

4.1 Описание процесса диагностирования

Процесс диагностирования начинается с того, что в базе данных определяются объекты, подлежащие диагностированию в соответствии с графиком ремонта. Рабочие места диагностики свя­заны проводной связью с компью­тером, проводящим оцифровку сигналов. Перед началом опера­ции диагностики инженер-электромеханик устанавли­вает датчик вертикально на чистую поверхность контролируемого объекта и подключает усилитель сигнала к линии связи. Датчик служит для преобразования механических колебаний в электрический сигнал. На выходе датчика преобразованные механические колебания имеют вид  аналогового временного сигнала. Но вследствие сложности формы временного сигнала, его интерпретация сильно затруднена, поэтому принято анализировать спектр сигнала, который является представлением временного сигнала в частотной области, для чего применяют быстрое преобразование Фурье (БПФ). В результате получается амплитудно-частотный спектр, который определяет распределение уровней вибрации в механизме по частотам.  

При диагностировании КМБ под локомотивом на ТР-1 колесная пара вывешивается гидравлическими домкратами  и далее для каждого КМБ последовательно собирается электрическая схема и подключается к источнику внешнего питания (стенду) для раскрутки КМБ.

При проведении технического диагностирования на ТР-3  КМБ (ТЭД) устанавливается на стенд (настил) с помощью крана. Перед  установкой  на  стенд  КМБ  проходит  подготовку  согласно  технологической  инструкции  по  ремонту  и  сборке  колесно-моторных  блоков (с косозубой передачей  - ТИ 179; с прямозубой передачей  -  ЦТ 4320).