Сложение чисел в МПТ: Методическое пособие к лабораторной работе

В методических указаниях излагаются теоретические основы базовой для вычислительной и микропроцессорной техники операции  – операции сложения.

1. Предварительные замечания

1.1. Основным узлом информационных систем, осуществляющим  арифметические операции, является сумматор с базовой функцией суммирования.

Через такую операцию реализуются другие арифметические операции, а именно

операция вычитания, интерпретируемая как операция сложения отрицательных операндов, представляемых в виде обратных или дополнительных кодов;

операция умножения, интерпретируемая как последовательность операций сдвигов множимого/множителя и сложений, обеспечивающих накопление суммы частичных (промежуточных)  произведений;

операция деления, интерпретируемая как последовательность операций вычитания (сложения делимого в дополнительном коде) с формированием очередной цифры частного

и т.д.

Функцию суммирования выполняет комбинационная схема, функционирование i–го разряда которой описывается таблицей соответствия (ТС) вида:

В таблице использованы следующие обозначения:  

CI (carry input) перенос из предыдущего разряда,  влияющий на значение формируемой суммы s;

CO (carry out) перенос в следующий разряд, возникающий при суммировании.

Таблицей описывается правило формирования одного разряда суммы s, учитывающее значения (биты) a, b слагаемых и бит переноса (СI) из младшего разряда. Кроме того, ТС задает правило формирования бита переноса CO в следующий разряд суммы.

Поэтому такой сумматор наз. полным одноразрядным комбинационным сумматором.

Из таблицы можно получить нормальные формы функций суммы s и переноса CO, которые  после упрощения представляются в виде:

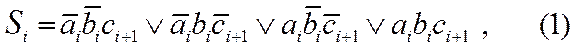На рисунке 1 приведена схема одноразрядного полного комбинационного сумматора, соответствующего выражениям (1),(2).

Одноразрядные сумматоры составляют основу для построения n–разрядных сумматоров, обеспечивающих сложение n – разрядных операндов (слагаемых).

На рисунках 2 и 3 приведены функциональные схемы n–разрядных сумматоров обратного и дополнительного кодов.

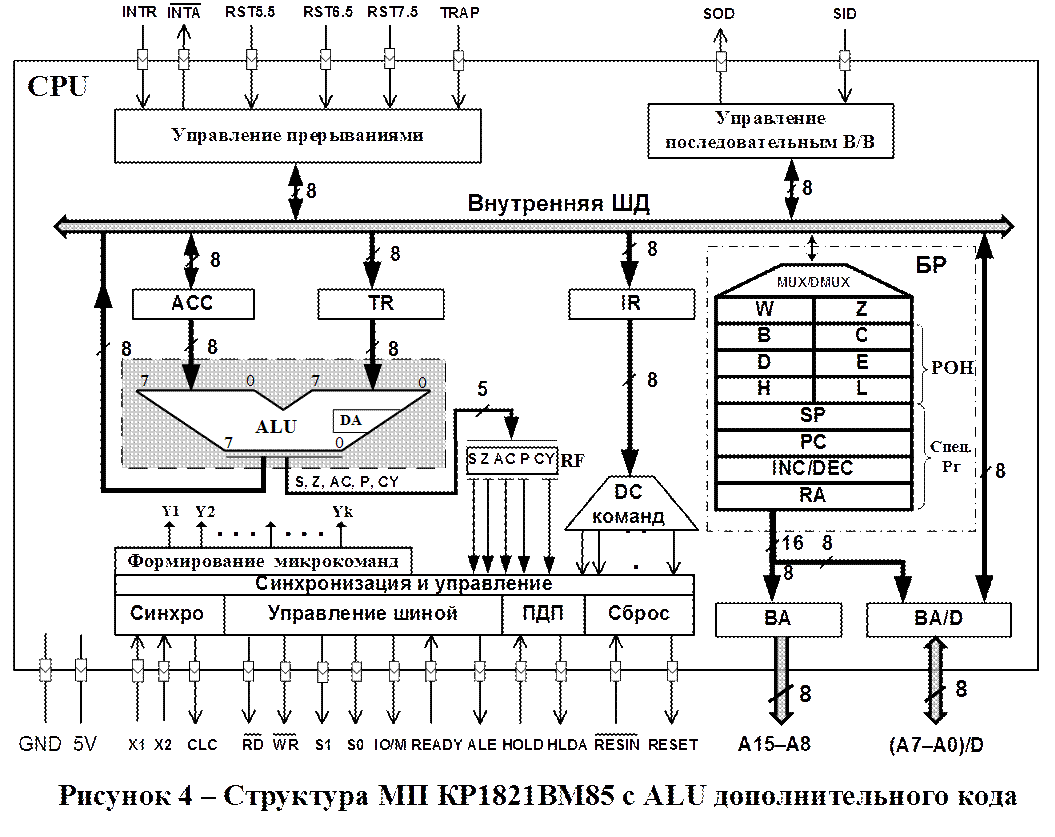
 В сумматоре дополнительного кода отсутствует связь циклического переноса из старшего (знакового) разряда в младший разряд. Это схемотехнически обеспечивает преимущества суммирования в дополнительных кодах. Сумматоры дополнительного кода являются основными функциональными частями арифметико–логических устройств (АЛУ) современных микропроцессоров. На рисунке 4 выделен восьмиразрядный сумматор дополнительного кода, используемый как основной блок АЛУ процессора I8085 (К1821ВМ85).

Применяя одноразрядные сумматоры в качестве базовых элементов, можно  реализовать сумматоры, обеспечивающие сложение двух и более операндов любой разрядности.

Пример 1 Выполнить сложение двух положительных восьмиразрядных двоичных чисел [A]_пр=0.0001010 и [B]_пр=0.0001110

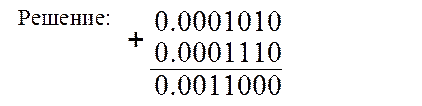Пример показывает, что сложение двух положительных чисел может быть выполнено непосредственно в прямых кодах. Проблемы возникают при обработке отрицательных операндов. Пути разрешения такой проблемы будут обсуждаться далее.

1.2  При сложении чисел необходимо учитывать форму их представления. Они могут складываться или как целые или как дробные числа. Такое представление наз. представлением в форме с фиксированной запятой.

Представление с ФЗ широко используется в МПТ.

В  этом формате в машинном  коде числа  запятой как символа – нет, однако, её положения известно “по умолчанию ”.

Обычно подразумевается, что запятая находится или после младшего разряда значащей части числа или перед  её старшим разрядом (после знакового).

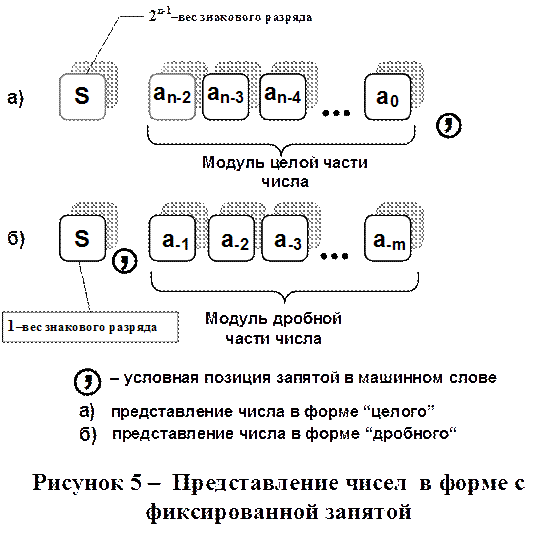В первом случае без изменения (по сравнению с исходными) могут быть представлены только целые числа,  во втором — только дробные, т.е. числа,  модуль которых не превосходит 1.

На рис.5 показан пример разрядной сетки ИС («формат данных») для представления двоичных чисел с фиксированной запятой в виде n-разрядного слова для случаев закрепления запятой после младшего разряда (формат а)) и (m+1)–разрядного слова для случаев закрепления запятой после знакового разряда(формат б)). 

В формате с ФЗ старший разряд  кода числа содержит один разряд кода знака (S- signum), остальные разряды кода числа – значащие, т.е. используются для представления кода модуля числа.

1.3. Применяя при  сложении форматы с фиксированной запятой необходимо контролировать  диапазон допустимых модулей суммы чисел.

Если результат операции превышает X_макс– т.е. максимально представимое в заданной разрядной сетке  и в используемом формате число, то возникает т.н. переполнение. Дальнейшее выполнение программы при переполнении не имеет смысла.

При известных длинах разрядной сетки можно определить диапазоны представимых в форме с фиксированной запятой сумм.

Очевидно, что поддиапазоны положительных и  отрицательных чисел симметричны относительно истинного нуля. Поэтому дальнейший анализ может быть выполнен для модулей представляемых чисел.

Дробные числа.

Максимальное по модулю положительное или отрицательное число содержит  во всех значащих разрядах единицы и отличается от 1 на единицу младшего разряда.