Сложение чисел в МПТ: Методическое пособие к лабораторной работе, страница 19

4. Обнаружение переполнения разрядной сетки в модифицированных дополнительных кодах

Модифицированные коды позволяют существенно упросить процедуру обнаружения переполнения разрядной сетки.

Исследование Случаев 1–5 позволяет так сформулировать признаки переполнения:

1.  признаком положительного переполнения является формирование комбинации 01 в знаковых разряде числа (“отрицательная” сумма);

2.  признаком отрицательного переполнения является формирование комбинации 10 в знаковых разряде числа (“положительная”  сумма).

3.  при сложении может возникнуть т.н. “особый случай переполнения”

  особый случай переполнения может возникнуть только при сложении отрицательных операндов (отрицательное переполнение) и только при использовании дополнительных кодов;

  “особый случай переполнения” не обнаруживается путем сравнения знаков операндов со знаком суммы, а требует особой процедуры;

  признаком переполнения такого типа является: а) комбинация 11 в знаковых разрядах суммы S_S=1; б) нулевое значение модуля суммы.

На рисунке 2 представлен алгоритм сложения чисел в дополнительных  модифицированных кодах.

Используется метод сравнения знаков.

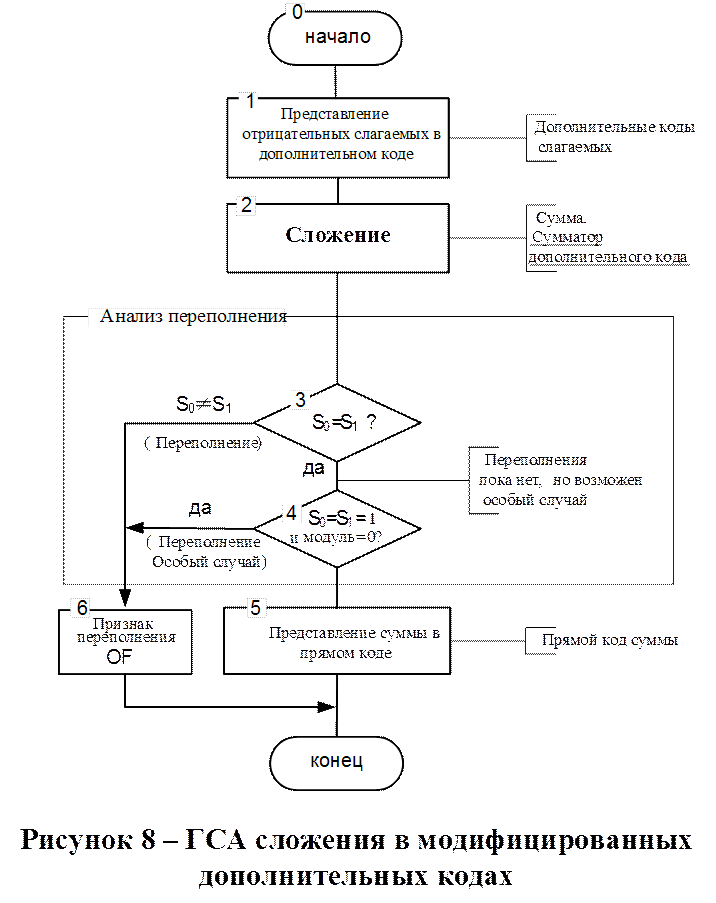Исходные предпосылки следующие:

1.  на входе сумматора поток чисел с произвольным знаком и произвольным модулем;

2.  отрицательные числа суммируются в дополнительном модифицированном коде

3.  в случае обнаружения переполнения алгоритм суммирования прерывается и формируется признак переполнения OF;

4.  вследствие использования дополнительных кодов, возможен “особый случай переполнения”.

Алгоритм предполагает, что возможны все случаи 1–9, рассмотренные ранее. Коротко комментируя алгоритм, необходимо отметить, что за анализом формальных признаков (знаки S_A,S_B,S_S слагаемых и суммы, а также величины модуля суммы) стоит логическая процедура соотнесения полученного результата суммирования с одним из случаев, рассмотренных ранее. Цель соотнесения – ответ на вопрос “ Переполнение есть?”.

В Блоке 3 алгоритма, путем сравнения знаков S_Aи S_B слагаемых А и В локализуются Случаи 6–9 (разные знаки операндов), при которых переполнение в принципе невозможно. Далее в Блоке 4, переход в который возможен только при равенстве знаков слагаемых S_A=S_B, путем сравнения знака любого слагаемого, например, S_A со знаком S_S суммы, локализуются Случаи 2,4 переполнения. Далее, путем совместного анализа на 0 модуля суммы и на единичное значение ее знакового разряда, Блоком 5 локализуется Случай 5 наличия особого переполнения. На выходе Блока5 –результат, соответствующий  Случаям 1,3 т.е. сумме без переполнения.

Рассмотренный алгоритм находит широкое практическое применение при реализации арифметических операций в средствах вычислительной и информационной техники.

Библиографический список

1.  Каган Б.Н. Электронные вычислительные машины и системы: Учеб. пособие для вузов. – М.: Энергия, 1973.– 528с., ил.

2.  Карцев М.А. Арифметика цифровых машин. М., «Наука», 1969.– 575 стр.

3.  Григорьев В.В. Кодирование чисел в микропроцессорных системах: Метод. указания. – ПГУПС, 2006.

4.  Григорьев В.В. Дополнительные коды при выполнении вычислительных операций: Метод. указания. – ПГУПС, 2008.

Содержание

                                                                                          стр.

1. Предварительные замечания..…………………………………………..1

2. Основные понятия и определения……………………………………...3

3. Случаи