2. отрицательные операнды должны быть преобразованы в дополнительные модифицированные коды и, в таком виде – суммироваться;
3. знаковые разряды слагаемых участвуют в операции наравне с числовыми разрядами;
4. перенос из старшего знакового разряда, который может возникнуть при сложении, должен быть игнорирован (отброшен),
5. если сумма – положительное число, то результат суммирования содержит нули в знаковых разрядах. Сумма в этом случае сформирована в прямом коде. Напротив, если сумма – отрицательна, то результат суммирования содержит единицы в знаковых разрядах, а сумма представлена в дополнительном коде;
6. при суммировании операндов одного знака возможно отрицательное или положительное переполнение. Признаком положительного переполнения является комбинация 01 значений в знаковых разрядах суммы. Признаком отрицательного переполнения является комбинация 10 в знаковых разрядах суммы
7. кроме того, при использовании дополнительных кодов возможен случай т.н. особого переполнения (особый случай переполнения).
Далее проводится анализ различных случаев сложения в дополнительных модифицированных кодах чисел, представленных в формате ФЗ.
На результаты сложения влияют
1. знаки слагаемых;
2. соотношения величин модулей слагаемых.
 |
|
Знаки слагаемых |
Знак/код знака |
Соотношение величин модулей слагаемых |
Возможность переполнения |
Случай |
Код знака суммы, как признак наличия/отсутствия переполнения |
Условия наличия/отсутствия переполнения |
|
|
A |
B |
||||||
|
Одинаковые |
+/00 |
+/00 |
несущественно |
возможно положительное переполнение |
1, переполнения нет |
переполнения нет, если “00” |
(A+B)<1 –для дроби (A+B)<2n-1 –для целого |
|
2, переполнение |
положительное переполнение, если “01“ |
(A+B) ³1 – для дроби (A+B)³2n- – для целого |
|||||
|
–/11 |
–/11 |
несущественно |
возможно отрицательное переполнение |
3, переполнения нет |
переполнения нет, если “11” |
|A|+|B|<1 – для дроби |A|+|B|<2n-1 – для целого |
|
|
4, переполнение |
отрицательное переполнение, если “10“ |
|A|+|B|³1 –для дроби |A|+B|³2n-1 – для целого |
|||||
|
–/11 |
–/11 |
существенно |
особый случай переполнения |
5, особый случай переполнения |
переполнение, если “11 “ и модуль суммы равен нулю |
|A|+|B|=1 –для дроби |A|+|B|=2n-1 – для целого |
|
|
Разные |
+/00 |
–/11 |
|A|>|B| |
переполнение невозможно |
6 |
“00“ |
переполнение невозможно |
|
+/00 |
–/11 |
|A|<|B| |
7 |
“11“ |
|||
|
–/11 |
+/00 |
|A| >|B| |
8 |
“11“ |
|||
|
–/11 |
+/00 |
|A| <|B| |
9 |
“00“ |
|||
Таблица 2 – Случаи сложения дробных и целых чисел в модифицированных ДК
3.2.1. Сложение дробных и целых положительных чисел без переполнения. (Случай 1)
3.2.1.1 Дробные числа.Пусть складываются два положительных слагаемых представленных в форме дробных чисел. Пусть также (A+B)<1. Очевидно, что сумма в этом случае – положительное число, представимое в заданной разрядной сетке т.е. переполнение в этом случае возникать не должно. Сумма должна быть сформирована прямом коде.
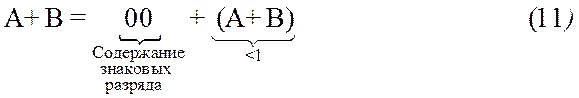 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.