Сложение чисел в МПТ: Методическое пособие к лабораторной работе, страница 2

Пример 2.Пусть  m =7. Тогда  |X_макс| =0.1111111. Подсуммирование единицы в младший разряд приводит к результату: 0,1111111 + 0.0000001 =1,0000000. Сумма равна единице, которая выходит за формат дробных чисел.

Справедливо

В формуле (3):   m – номер младшего разряда машинного слова (Рис.5)

Таким  образом, переполнение разрядной сетки при сложении дробных чисел  описывается условиями  

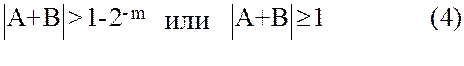Целые числа.

Максимальное по модулю положительное или отрицательное целое число содержит во всех значащих разрядах единицы. 

Поэтому справедливо

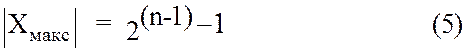С учетом (5), переполнение разрядной сетки при сложении целых чисел  описывается условиями  

  Из соотношений (3) и (6) вытекают следующие определения.

Переполнение разрядной сетки – случай при сложении, когда модуль суммы превышает максимальное число, представимое в заданной разрядной сетке;

Переполнение возможнотолько при сложении чисел одного знака, так как  модуль суммы в этом случае всегда превышает модули ненулевых слагаемых;

Переполнение невозможно при сложении  чисел разных знаков. Модуль суммы в этом случае меньше модуля максимального и представимого в заданной разрядной сетке слагаемого;

Переполнение, возникающее при сложении двух отрицательных операндов наз. отрицательным переполнением, а  переполнение, возникающее при сложении двух положительных операндов – положительным.

3. Сложение чисел в простых кодах

Следует различать процедуры сложения в простых и модифицированных кодах.

В простых кодах для кодирования знака используется один старший разряд кода.

В модифицированных кодах для кодирования знака используется два разряда кода.

Ниже, в этом разделе  рассматриваются особенности сложения в простых дополнительных и обратных кодах, а затем в разделе 4 сложение в модифицированных кодах.

3.1. Процедура сложения чисел в простых дополнительных кодах    (ПДК)

Процедура1. Основные правила сложения в простых дополнительных кодах:

1.  положительные операнды участвуют в сложении в прямых кодах;

2.   отрицательные операнды должны быть преобразованы в дополнительные коды и, в таком виде – суммироваться;

3.  знаковый разряд слагаемых участвует в операции наравне с числовыми разрядами;

4.  перенос из знакового разряда, который может возникнуть при сложении, должен быть игнорирован (отброшен);

5.  при суммировании операндов одного знака возможно отрицательное или положительное переполнение;

6.  при сложении может формироваться либо положительная, либо отрицательная сумма. При этом:

6.1 если сумма – положительное число, а  переполнение отсутствует, то она содержит “0” в знаковом разряде и  представлена в  прямом коде.

6.2 если сумма – отрицательна, то результат суммирования содержит единицу в знаковом разряде, а сумма представлена в дополнительном коде;

7.  при использовании дополнительных кодов возможен случай т.н. особого переполнения (особый случай переполнения).

Далее проводится анализ различных случаев сложения (Процедура 1) в дополнительных простых кодах чисел, представленных в форматах дробных и целых чисел. Таблица 1, строится исходя из того, что на результаты сложения влияют

1.  знаки слагаемых;

2.  величины модулей слагаемых и их соотношение.

Учитывается то, что при сложении  возможно переполнение результата, определяются признаки таких ситуаций. Выделены по перечисленным признакам девять случаев, которые могут иметь место при сложении. В последующий разделах каждый случай проанализирован с точки зрения возможности его возникновения, особенностей получаемых результатов и последствий.

3.1.1. Сложение дробных и целых  положительных чисел без  переполнения. (Случай 1)

3.1.1.1 Дробные числа.Пусть складываются два положительных слагаемых представленных в форме дробных чисел. Пусть также (A+B)<1.

Очевидно, что сумма в этом  случае – число, представимое в заданной разрядной сетке т.е. переполнение в этом случае возникать не должно. Слагаемые представляются в прямых кодах, а сумма также должна быть сформирована прямом коде и иметь признаки положительного числа.