Сложение чисел в МПТ: Методическое пособие к лабораторной работе, страница 12

3.6.Сложение в обратных кодах чисел разных знаков

Рассматриваемые ниже случаи  сложения чисел разного знака имеют следующие особенности

1.  при сложении  чисел разных знаков переполнение невозможно. Модуль суммы в этом случае всегда меньше модуля максимального и представимого в заданной разрядной сетке слагаемого;

2.  знак суммы зависит, в отличие от ранее рассмотренных случаев, не только от знаков слагаемых, но и от соотношения их модулей.

3.  в зависимости от соотношения модулей, сумма может формироваться или в прямом или в обратном кодах.

3.1.6.1. Модуль положительного операнда больше модуля отрицательного. (Случаи 6, 9)

Пусть, А,В – операнды, отвечающие соотношениям 

для случая 6: А ³0 и В£0. Кроме того, | А |³| В |.

для случая 9: A£ 0 и B³0 Кроме того, | А |£ | В |

Выполняемое сложение при этих  условиях эквивалентно соответственно вычитаниям (А– В)  и (В–А). Разность, априори, положительна. Отрицательный операнд складывается в обратном коде.

В обоих случаях должен возникать подсуммируемый в младший разряд суммы перенос.

Как для дробных, так и для целых чисел в результате сложения в обеих рассматриваемых случаях должен формироваться прямой код положительной разности.

Пример 4–ОК.  Сложение дробных  и целых  чисел разного знака.  Модуль положительного операнда больше модуля отрицательного (Случаи 6,9)
Выполнить сложение в обратном коде пар дробных и целых отрицательных операндов соответственно А,В и X,Y.
	Дробные слагаемые равны	Целые слагаемые равны
	А=0,510=   0,1000002; В= –0,062510 = –0,00010002;	X=–1910 = –0 00100112; Y= 5110 =   0 01100112;
Предварительные выводы. Предварительное сложение приводит к результатам         A+B=0, 510 –0,062510=0,4375 10=0,01110002;  X+Y= –1910+5110= 3210.= 0 01000002. Должны быть  получены положительные суммы, представленные в прямом коде.
Кроме того, следует ожидать переносы из знаковых разрядов дробных и целых сумм.
Решение. Отрицательные операнды преобразуются в обратный код.
	Обратный код дробного слагаемого В равен	Обратный код целого слагаемого X равен
	[В]обр=1.11101112	[X]обр=1 11011002
Сложение в двоичных обратных кодах имеет вид:
Получены правильные результаты, что подтверждает теоретические выводы.

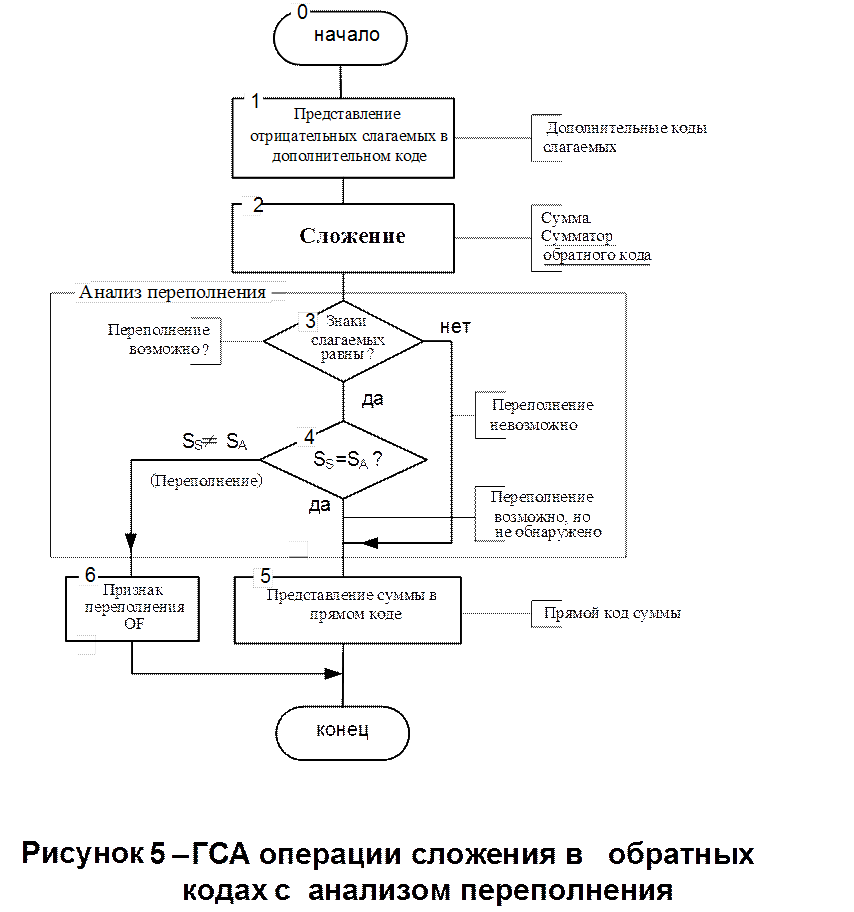
3.4 Обнаружение переполнения разрядной сетки в ПОК

На рисунке 3  представлен алгоритм обнаружения переполнения путем сравнения знаков. Алгоритм аналогичен по логической структуре с рассмотренным ранее  алгоритмом обнаружения переполнения для дополнительных кодов. Отличие состоит в отсутствии проверки на особый случай переполнения разрядной сетки, что является преимуществом обратных кодов.

 

4. Cложение чисел в модифицированных дополнительных кодах  (МДК)

Модифицированные коды упрощают процедуру обнаружения переполнения.

В модифицированных кодах для кодирования знака используются не один, как в простых кодах а два разряда S₀, S₁. т.е. для представления слагаемого вводится дополнительный разряд. (Рис.5)

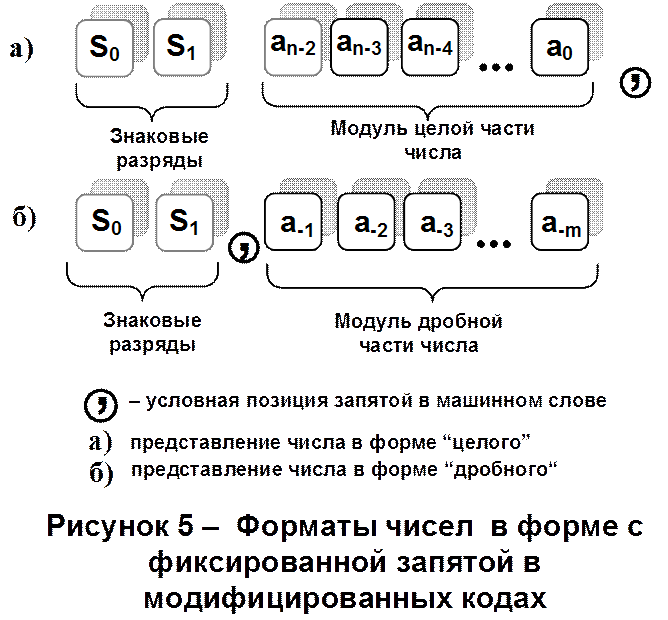Комбинация значений “00” используется как код знака  “+”, а комбинация “11” как код знака  “–”. В модифицированном коде может быть представлен как прямой, так и обратный и дополнительный коды (Рис.6).

Процедура 3. Основные правила сложения в модифицированных дополнительных кодах:

1.  положительные операнды участвуют в сложении в прямых модифицированных кодах;