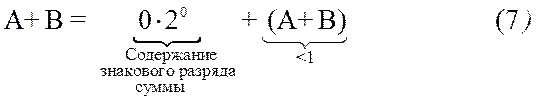 |
Соотношения (7) интерпретируется следующим образом. Вследствие ограничения (А+В)<1 при сложении отсутствует перенос CY из старшего разряда модуля суммы в знаковый разряд. Такой перенос мог бы повлиять на значение знака суммы. Тогда, содержимое знакового разряда результата определяется суммой SA+SB+ CY =0*20+0*20+0=0. Таким образом, в отсутствии переноса, сумма – положительное число, представленное в прямом коде с нулевым знаковым разрядом, а переполнение отсутствует.
3.1.1.2 Целые числа.Пусть складываются два положительных слагаемых представленных в форме целых чисел. Пусть также (A+B)<2n-1. Сложение выполняется в прямых кодах. Очевидно, что сумма в этом случае должна быть положительным числом, переполнения возникать не должно, а сумма должна быть сформирована прямом коде.
Аналитически этот случай описывается как
Таблица 2 – Случаи сложения дробных и целых чисел в простых дополнительных кодах
|
Знаки слагаемых |
Знак |
Соотношение величин модулей слагаемых |
Возможность переполнения |
Случай |
Условия наличия/отсутствия переполнения |
Знак суммы, какпризнак наличия/отсутствия переполнения |
|
|
A |
B |
||||||
|
Одинаковые |
+ |
+ |
несущественно |
возможно положительное переполнение |
1, переполн. нет, сумма положит. |
(A+B)<1 –для дроби (A+B)<2n-1 –для целого |
“+“, совпадает со знаками слагаемых |
|
2, пол. переполнение |
(A+B) ³1 – для дроби (A+B)³ 2n-1 –для целого |
“–“, противоположен знакам слагаемых |
|||||
|
– |
– |
несущественно |
возможно отрицательное переполнение |
3, переполн. нет, сумма отрицат. |
|A+B|<1 –для дроби |A+B|<2n-1 –для целого |
“–“, совпадает со знаками слагаемых |
|
|
4, отр. переполнение |
|A+B|³1 – для дроби |A+B|³2n-1 – для целого |
“+“, противоположен знакам слагаемых |
|||||
|
– |
– |
|A|+B|=1 –для дроби |A|+|B|=2n-1 – для целого |
особый случай переполнения |
5, особый случай переполнения |
|A|+|B|–1= 0 –для дроби |A|+|B|–2n-1= 0 – для целого |
“–“ , совпадает со знаками слагаемых |
|
|
Разные |
+ |
– |
|A|>|B| |
переполнение невозможно |
6, сумма положит. |
Переполнение невозможно, а соотношение модулей слагаемых определяет знак суммы |
“+” |
|
+ |
– |
|A|<|B| |
7, отриц. |
“–“ |
|||
|
– |
+ |
|A|>|B| |
8, отриц. |
“–“ |
|||
|
– |
+ |
|A|<|B| |
9, сумма положит. |
“+” |
|||
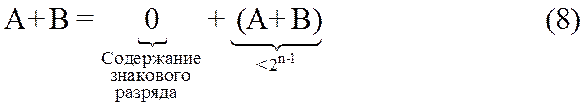 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.