Сложение чисел в МПТ: Методическое пособие к лабораторной работе, страница 8

3.4 Обнаружение переполнения разрядной сетки в ПДК

Для обнаружения переполнения в настоящее время используются следующие способы:

-  сравнение знака суммы со знаками операндов.

Работоспособность этого способа, подтвержденна ранее теоретически и проиллюстрированный на примерах 1–7. 

В силу прстоты он находит широкое практическое  применение. Исследование Случаев 1–5 позволяет так сформулировать признаки  возникающего переполнения:

1.  признаком положительного переполнения, если слагаемые положительные числа, является единица в знаковом разряде суммы (“отрицательная” сумма);

2.  признаком отрицательного переполнения, если слагаемые отрицательные числа, является нуль в знаковом разряде суммы (“положительная”  сумма).

Особые выводы следуют при  “особом случае” переполнения

1.  при сложении в ПДК может возникнуть т.н. “особый случай переполнения”

2.  особый случай переполнения может возникнуть только при сложении отрицательных операндов (отрицательное переполнение) и только при использовании дополнительных кодов;

3.  “особый случай переполнения” не обнаруживается путем сравнения знаков операндов со знаком суммы, а требует особой процедуры;

4.  признаком переполнения такого типа является а) единичное значение в знаковом разряде суммы S_S=1 б) нулевое значение модуля суммы;

5.  обнаружение   “особого случая переполнения”, требуют анализа двух признаков результата, что усложняет алгоритмы сложения чисел в дополнительном простом коде.

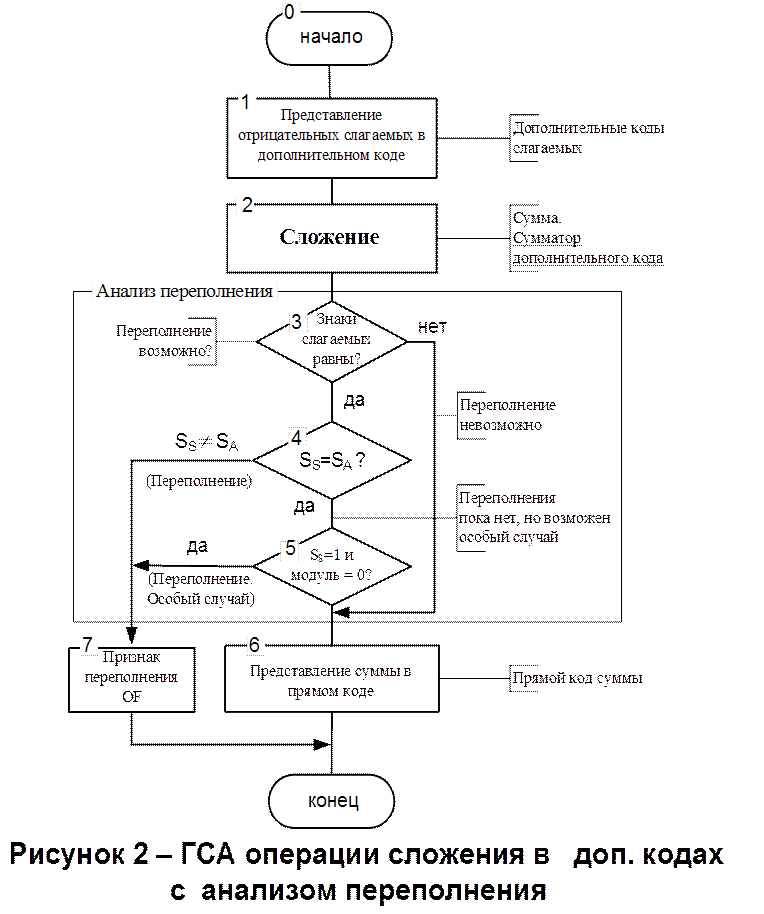
На рисунке 2 изображен алгоритм сложения чисел в дополнительных простых кодах.

В алгоритме в упрощенном виде представлены: блок преобразования слагаемых в дополнительные коды (блок 1), блок суммирования (блок 2)  и блок  преобразования полученной суммы в прямой код (блок 6).

Более детально раскрыта процедура анализа переполнения. Используется метод сравнения знаков суммы со знаками слагаемых .

Исходные предпосылки следующие:

1.  на входе сумматора – поток чисел с произвольным знаком и произвольным модулем;

2.  отрицательные числа преобразуются в дополнительный  код

3.  в случае обнаружения переполнения алгоритм суммирования прерывается и формируется признак переполнения OF (Overflow Flag)

4.  вследствие использования дополнительных кодов, возможен “особый случай переполнения”.

Алгоритм предполагает, что возможны все рассмотренные случаи 1–9.

Коротко комментируя алгоритм, необходимо отметить, что за анализом формальных признаков (знаки S_A,S_B,S_S слагаемых и суммы, а также величины модуля суммы) стоит логическая процедура соотнесения полученного результата суммирования с одним из случаев, рассмотренных ранее. Цель соотнесения – ответ на вопрос “ Переполнение есть?”.

В Блоке 3 алгоритма, путем сравнения знаков S_Aи S_B слагаемых А и В обнаруживается Случаи 6–9 (разные знаки операндов), при которых переполнение в принципе невозможно. Далее, в Блоке 4, переход в который возможен только при равенстве знаков слагаемых S_A=S_B, путем сравнения знака любого слагаемого, например, S_A со знаком S_S суммы, обнаруживаются Случаи 2,4 переполнения. Далее, путем совместного анализа на 0 модуля суммы и на единичное значение ее знакового разряда, Блоком 5 обнаруживается Случай 5 особого переполнения. На выходе Блока5 –результат, соответствующий  Случаям 1,3 т.е. сумме без переполнения.

Рассмотренный алгоритм находит широкое практическое применение при реализации арифметических операций в средствах вычислительной, микропроцессорной  и информационной техники.

3.2. Cложение чисел в простых обратных  кодах  (ПОК)

Сложение в простых обратных кодах основано на следующих правилах.

Процедура СлОК. Основные правила сложения в простых обратных кодах:

1.  положительные операнды участвуют в сложении в прямых кодах;

2.  отрицательные операнды должны быть преобразованы в обратные простые коды и, в таком виде – суммироваться;