Информатика и выч. техника \ Основы микропроцессорной техники и прикладное программирование

Сложение чисел в МПТ: Методическое пособие к лабораторной работе, страница 4

Пример 1Сложение дробных и целых  положительных     чисел  без   переполнения (Случай 1)

         Выполнить в ПДК  сложение дробных А,В и целых X,Y положительных операндов. 

Дробные слагаемые равны

Целые слагаемые равны

А= 0.742187510=0.10111112;

В= 0,187510         = 0.00110002,

X= 3710 = 0 01001012;

Y= 2410 = 0 00110002.

         Предварительное решение. При заданных значениях слагаемых, суммы (А+В) и (X+Y) должна быть равны, соответственно  

        (А+В) =0.929687510   ®0.11101112  и  (X+Y) = 6110  ®0 01111012.

        Предварительные выводы. Полученные суммы  не превосходят максимальных значений чисел, представимых на заданной разрядной сетке т.е 1 для дробного числа и 127 для целого. Таким образом, при заданных слагаемых переполнения возникать не должно.

        Решение. Так как все слагаемые положительные числа, то они представляются непосредственно в прямых кодах.

        Сложение в двоичных простых прямых кодах имеет вид:


Таким образом, результаты – положительные суммы без переполнения,  сформированные в прямом коде, что подтверждает условия (7), (8). Признаком отсутствия переполнения является знак суммы, совпадающий со знаком слагаемых.


3.1.2. Сложение дробных и целых положительных чисел с переполнением (Случай 2)

               3.1.2.1 Дробные числа. Пусть складываются два положительных слагаемых представленных в форме дробных чисел. Пусть также (A+B)³1. Очевидно, что сумма в этом  случае превосходит максимальное число,  представимое в заданной разрядной сетке, т.е. должно иметь место переполнение, признаком которого должен стать отрицательный знак суммы. Так как слагаемые положительные числа, то сложение выполняется в прямых кодах.

Особенности этого случая сложения могут быть пояснены  аналитическим выражением


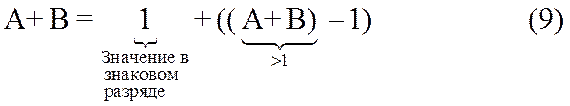Из (9) следует, что: так как (А+В)³ 1, то при  сложении формируется перенос CY в знаковый разряд из старшего разряда модуля суммы. Перенос  влияет  на значение знака суммы. Поэтому, содержимое знакового разряда определяется суммой SA+SB+ CY =0+0+1=1. Таким образом, сумма – число, в знаковом разряде которого 1, а в значащих разрядах разность (A+B) –1.

3.1.2.2. Целые числа.Пусть складываются два положительных слагаемых, представленных в форме целых чисел. Пусть также (A+B)³2n-1. Очевидно, что в этом  случае, также как и при сложении дробных чисел, должно иметь место положительное переполнение разрядной сетки, признаком которого служит  отрицательный знак суммы. Так как слагаемые положительные числа, то сложение выполняется в прямых кодах.


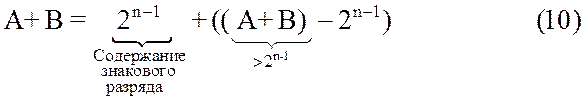Аналитически сложение описывается как.

Так как  (A+B)³2n-1,то при  сложении формируется перенос CY в знаковый разряд из старшего разряда модуля числа. Перенос  влияет  на значение знака суммы. Действительно, содержимое знакового разряда определяется как SA+SB+ CY =0+0+1=1. Таким образом, сумма – число, в знаковом разряде которого 1, а в значащих разрядах остаток (A+B) –2n-1.


 Пример 2.Сложение дробных и целых положительных чисел с переполнением (случай 2)

Выполнить в ПДК  сложение соответственно дробных А, В и целых X,Y положительных операндов.

Дробные слагаемые равны

Целые слагаемые равны

А=0,687510=0.10110002;

В=0.437510=0.01110002

X= 6410= 0 10000002;

Y=7610 =0 10011002

         Предварительное решение. При заданных значениях слагаемых, суммы (А+В) и (X+Y) должна быть равны, соответственно  

         (А+В) =1.125 0®1.00100002  и  (X+Y)=14010®1 00011002.

         Предварительные выводы. Полученные суммы  превосходят максимальные значения чисел, представимых на заданной разрядной сетке т.е 1 для дробного числа и 127 для целого. Таким образом, при заданных слагаемых должно возникнуть  переполнение.

Признаком переполнения должно быть единичное значение в знаковых разрядах.

        Решение. Так как все операнды положительные числа, то они складываются непосредственно в прямых кодах.

        Сложение в двоичных простых прямых кодах имеет вид:


Таким образом, результаты – суммы с переполнением.  Признаком переполнения является знак суммы, противоположный знаку слагаемых.

Скачать файл