Введение в системы счисления. Методы конвертирования: Методическое пособие к лабораторной работе № 1

последовательности имеет позиции k=0; 3) остальные n-b цифр цисла равны 0.

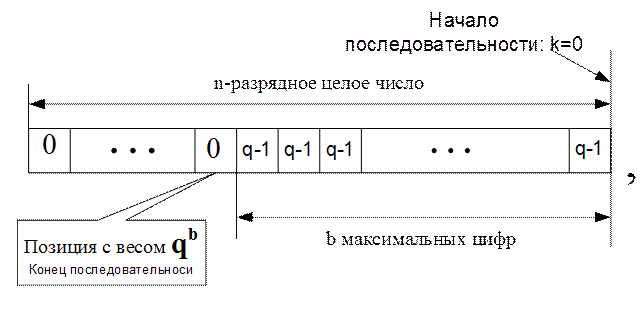Тогда количественный эквивалент такого числа определяется как

или

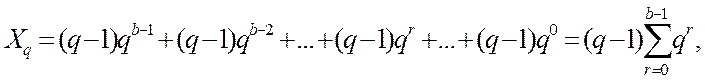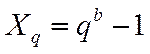Пример 1. Доказать, что 8-ми разрядное целое десятичное число X¹⁰, определенное разностью 10⁶–1 имеет числовой эквивалент 00999999d.

Решение. Степень 10⁶ –десятичное  число 01000000. Тогда разность

10⁶–1 равна 0999999d.

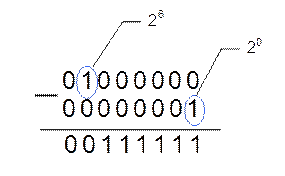
Пример 2. Определить десятичный  эквивалент 8-разрядного целого двоичного числа X₂=00111111b.

Решение. Согласно Свойству 7, при b=6 и k=0  X₂= 2⁶–1=63₁₀.

Для проверки полученного результата можно выполнить вычисление суммы полиномиального разложения, соответствующего исходному числу

2⁵+2⁴+2³+2²+2¹+2⁰=63₁₀

Другая проверка поясняет сущность операции вычитания 2⁶–1

Замечание 1.

Очевидно, что при в = n,  то

Таким образом, Свойство 1 является частным случаем Свойства 8.

Замечание 2. Свойство 7 позволяет упростить реализацию арифметических операций.

Например, может быть упрощен  перевод двоичных чисел соответствующих условиям Свойства 8 в десятичную систему счисления. Замена суммирования b членов полиномиального ряда вычислением разности qⁿ–1 приводит к упрощению вычислений. Причем, выигрыш в упрощении  тем больше, чем  длиннее последовательность.

Свойство 9.

Пусть  q-значное n-разрядное целое число X_q содержит последовательность из b максимальных в этой системе счисления цифр(b£ n).

Младшая цифра последовательности занимает  k-ую (n-1 ³k³ 0) позицию в числе, т.е.

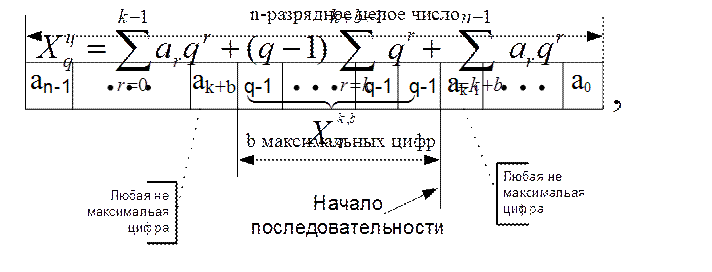Тогда количественный эквивалент числа определяется как

а количественный эквивалент последовательности  как

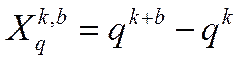Пример3. Определить количественный эквивалент последовательности из 6-ти максимальных цифр в  9-ти разрядном десятичном числе

X₁₀ =9369999954D.

Согласно  заданное число можно представить  как  9360000000+(10⁷–10²)+0000000054.

При этом разность (10⁷–10²⁾ оценивает  количественный эквивалент последовательности из 6-ти девяток, младшая цифра которой занимает  вторую позицию в числе

Разность “в столбик” определяется  как 

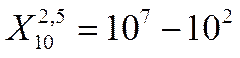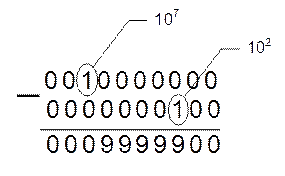Тогда  X¹⁰ =9360000000+0009999900+0000000054=9369999954, что подтверждает справедливость  Свойства 8.

Пример 4.Определить количественный эквивалент последовательности из 7-ми максимальных цифр в  12-ти разрядном двоичном числе

X₂ =100111111101b.

Согласно  заданное число можно представить  как 10000000000+(2⁹-2²)+000000000001.

Количественный эквивалент последовательности в десятичной системе счисления определяется путем вычисления разности (2⁹-2²). Степени равны  2⁹=512 и 2²=4, а их разность (2⁹-2²)=512 - 4=508.

Использование вычислений в “столбик” приводит к результату

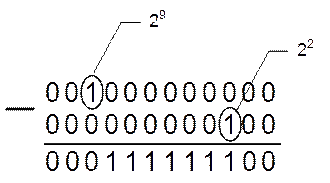В результате последующего суммирования 100000000000+000111111100+00000000001=100111111101b получается исходное число, что подтверждает справедливость  Свойства 9.

Свойство 10. Пусть  дробная часть q-значного n-разрядного числа Xq состоит из b максимальных в этой системе счисления цифр. При этом b£m.

Начальные условия  поясняются рисунком.

Очевидно, что

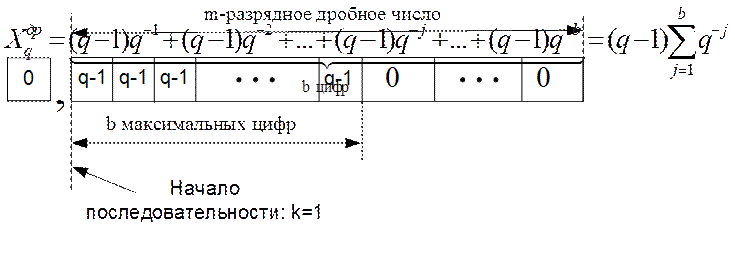Тогда при введенных условиях Свойство 9 состоит в следующем

или

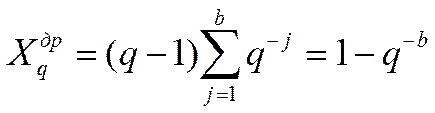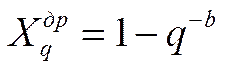Пример5. Определить количественный эквивалент 16-ти разрядного дробного  двоичного числа 0,111111100000000b, дробная часть которого состоит из  7-ми максимальных цифр.

Решение. Согласно ( )  заданное число  X2 =0,111111100000000b, представляется как X₂= 1– 2^–7=(128-1)/128=0,9921875.

Пример 6.Подтвердить, что разность 1– 2^–9 задает двоичное дробное число 0,11111111100.

Решение. 2^–9=0,000000001. Вычитание в “столбик” приводит к результату

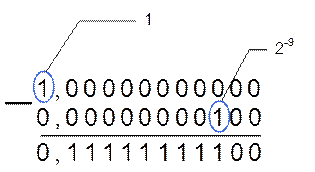Таким образом, разность 1– 2^–9 = 0,11111111100. Это подтверждает условие примера.

Свойство 11.

Пусть  q-значное m-разрядное дробное число Xq содержит последовательность из b максимальных в этой системе счисления цифр(b£m).

Старшая цифра последовательности занимает  k-ую позицию в числе. Условия, для которых определено Свойство 11 иллюстрируются рисунком

                                                                                                                                                                                   

Очевидно, что справедливо представление заданного числа в виде

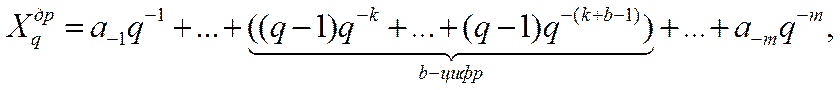
а далее

Количественный эквивалент X^k,b задается соотношением

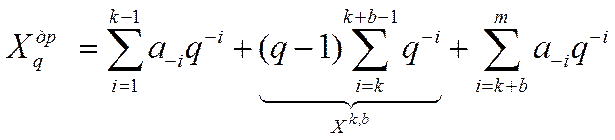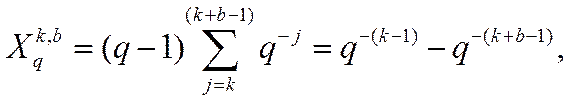          Таким образом, свойство 11 состоит в следующем:

Количественный эквивалент последовательности из b максимальных цифр, старшая из которых занимает k-ую позицию в дробном q-ичном числе