Диагностирование логических схем на функциональных элементах, страница 6

          Для константных неисправностей функция, реализуемая неисправным элементом, может быть получена из функции исправного элемента фиксацией в 0 или 1 ее переменных. Например, для элемента ИЛИ-НЕ (рис. 4.3) функция неисправности  для случая обрыва резистора

 = .

4.3. Методы построения тестов для комбинационных схем

          В данном разделе рассматриваются вопросы синтеза тестов для константных неисправностей. Такие тесты обеспечивают также обнаружение значительного числа неисправностей другого типа, которые в § 4.1 определены как неконстантные неисправности.

4.3.1. Метод таблицы функций неисправностей

          Для построения проверяющего теста вычерчивается схема с указанием всех логических элементов и связей между ними. Записывается реализуемая схемой функция в виде формулы, отражающей структуру схемы. Комбинационная схема (рис. 4.11)

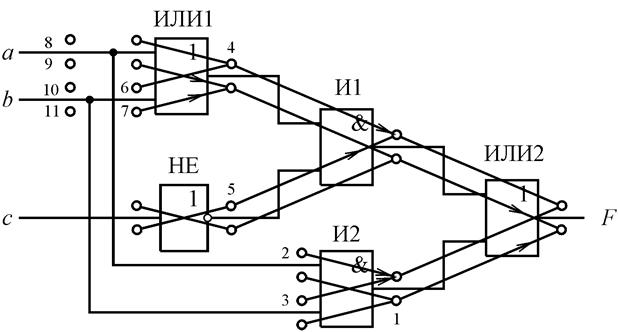
Рис.4.11.

 реализует функцию

.                                     (4.2)

На схеме указываются неисправности компонент. Под компонентами схемы понимают входы и выходы элементов и входы схемы. Если выход элемента или входы схемы соединен со входом только одного элемента или только с одним выходом схемы, то это соединение рассматривается как одна компонента. Если в схеме имеется точка разветвления, то в качестве компонент выступают как точка разветвления, так и все ветви разветвления. Для каждой компоненты указывают две константные неисправности К.0 и К.1. Рассматриваемая схема имеет 12 компонент и 24 неисправности.

          Для каждого логического элемента наносится граф эквивалентных неисправностей и указываются отношения импликации между неисправностями, в результате чего устанавливаются отношения между неисправностями для всей схемы. Неисправности нумеруются, причем среди эквивалентных неисправностей нумеруют только одну, ближе всех расположенную к выходу (для нее наиболее просто вычислить проверяющую функцию); все неисправности, к которым направлены дуги, не нумеруются; если хотя бы к одной из эквивалентных неисправностей направлена дуга, то ни одну из них не нумеруют. В результате данной операции сокращают список неисправностей, которые необходимо рассматривать при построении проверяющего теста. Пронумерованные неисправности образуют контрольное множество неисправностей . В данной схеме пронумеровано 11 неисправностей, в то время как исходное множество содержит 24 неисправности.

          Составляется ТФН (табл. 4.5), в которую включаются все неисправности из множества . Функции неисправности рассчитываются двумя способами. Первый из них предусматривает внесение рассматриваемой неисправности в схему, и определение функции, реализуемой этой схемой. Например, неисправность 4 фиксирует на выходе элемента ИЛИ1 сигнал К. 1. На рис. 4.12 приведена неисправная схема, по структуре которой определена функция неисправности .

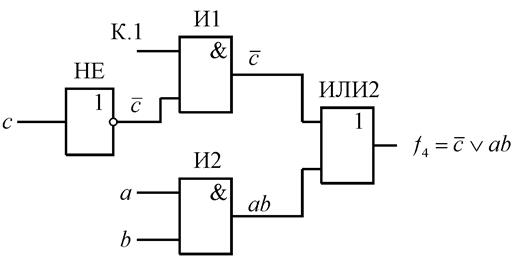
Рис.4.12.

Второй способ заключается в проецировании неисправностей на формулу, отражающую структуру схем. Так указанная неисправность связана с элементом ИЛИ1, который реализует входящую в формулу (4.2) скобку (). Следовательно, для получения функции  необходимо в формуле (4.2) данную скобку зафиксировать в единицу. Тогда получим

 = .

          По ТФН при помощи метода, изложенного в разделе 1.4, вычисляется проверяющий тест . Кроме того, так как в данном случае объектом исследования является логическая структура, то при вычислении могут быть использованы следующие формулы.

Т а б л и ц а   4.5