Диагностирование логических схем на функциональных элементах, страница 11

          D-алгоритм  состоит  из  двух  этапов [45]: 1. D-продвижение. 2. Обратное доопределение. На первом этапе осуществляется «продвижение» символа D на выход схемы, т.е. создается хотя бы один существенный к неисправности D-путь. Для этого рассматриваются все возможные пути от места неисправности до выхода схемы. В данном случае надо рассмотреть два пути: 6–9–12–14 и 6–10–13–14.

          Записывается расширенный D-куб неисправности. При этом предполагается, что все координаты, кроме уже определенных в основном кубе, равны х:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
	х	0	0	х	х	D	х	х	х	х	х	х	х	х  .

          Задача D-алгоритма заключается в том, чтобы в соответствии с логикой схемы заменить неопределенные координаты х на символы из множества  так, чтобы выходная линия схемы имела символ D или .

          Вводится операция D-пересечения (обозначается символом ) над элементами из множества . Пусть . Тогда операция D-пересечения задается следующими равенствами:

          1)  (совпадение сигналов);

          2)  (доопределение сигнала);

          3) Æ, если ,  и .

Символ Æ означает, что пересечение является пустым (или противоречивым).

          Операция D-пересечения над кубами  и  состоит в применении операции D-пересечения над одинаковыми координатами векторов  и . Пересечение     является пустым (противоречивым), если хотя бы одна координата вектора      равна  Æ.

          Рассмотрим путь 6–9–12–14 и определим, является ли он существенным для неисправности . Определим условия, когда символ  может появиться на линии 9 (см. рис. 4.21).

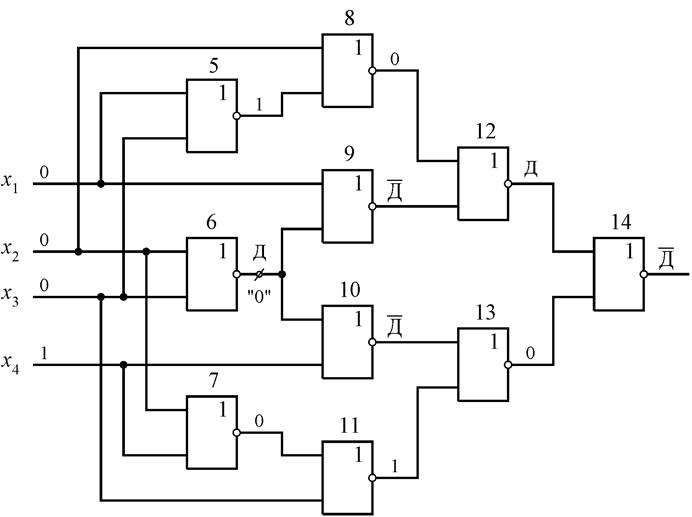
Рис.4.21.

 Эти условия определяются указанием значений сигналов на линиях 1, 2, 3, 6, 9. Находятся непустые пересечения D-куба неисправности  и всех D-кубов элемента 9. Последний является элементом ИЛИ-НЕ и имеет 6 D-кубов

          Вектор пересечения куба  и D-куба элемента 9 № 1 имеет вид:

Пересечение является пустым, т.к. координата 6 = Æ. Это означает, что существует противоречие: на линии 6 должен быть сигнал D (по условию куба ) и в то же время – сигнал 0 (по условию куба ).

          Пустыми являются также пересечения куба  и D-кубов с номерами 2, 3, 5. Два куба пересечения не являются пустыми:

=	1 2 3  6   9	,	=	1  2  3   6  9
	00 0D			D0  0 D  .

Куб  имеет для входной линии 1 значение D. Однако, входная линия должна быть определена как 0 или 1. Поэтому выполняется замена у входных линий символа D на символ 0 (т.к. D = 1  0), а символа  на символ 1 (т.к. D = 0  1). После такой замены куб  совпадает с кубом . В результате существует один куб

который определяет следующее условие трансляции неисправности  на выход элемента 9: на линиях 1, 2 и 3 должны быть сигналы 0.

          Далее осуществляется описанная процедура последовательно для всех элементов рассматриваемого пути вплоть до выходного элемента схемы. В данном случае рассматривается элемент 12, при этом находятся непустые пересечения полученного выше куба  и D-кубов элемента 12: