Диагностирование логических схем на функциональных элементах, страница 17

Т а б л и ц а   4.11

          Таким образом, справедливо

          Утверждение 4.1. Короткое замыкание между линиями логической схемы искажает работу схемы только тогда, когда в исправной схеме на этих линиях формируются различные логические сигналы.

В схеме на рис. 4.32 при КЗ между линиями 1 и 2 логический сигнал 0 доминирует над логическим сигналом 1. Это значит, что если на одной из этих линий устанавливается сигнал 0, то этот же сигнал устанавливается и на второй линии независимо от того, в каком состоянии находится транзистор, к которому подключена вторая линия. Логический сигнал 1 может установиться на обеих линиях только в том случае, когда этот сигнал формируется в исправной схеме также на обеих линиях. Поэтому КЗ между линиями 1 и 2 эквивалентно внесению в схему дополнительного элемента И (монтажное И). На рис. 4.33 приведены логическая структура, соответствующая схеме рис. 4.32, и ей эквивалентная схема с КЗ.

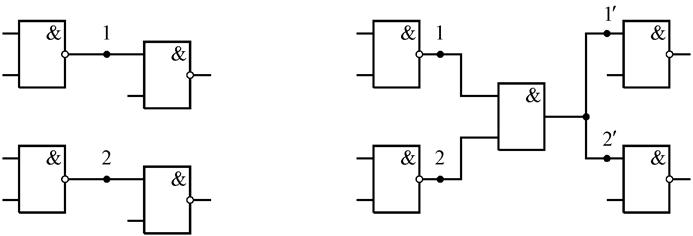
Рис.4.33.

 В том случае, когда используется логика, в которой логический сигнал 1 доминирует над логическим сигналом 0, в схеме рис. 4.33,б дополнительный элемент И заменяется на элемент ИЛИ.

          Рассмотрим одиночное КЗ без ОС между линиями с номерами  и . Введем обозначения:  – проверяющая функция неисправности ;  – кратная неисправность,  состоящая из неисправностей типа «константа 0» линий  и ;  – проверяющая функция неисправности ;  и  – функции, реализуемые на линиях  и  в исправной схеме.

          Сравним поведение схемы с неисправностью  и поведение схемы с дополнительным элементом И, которая эквивалентна схеме с КЗ (см. рис. 4.33). Отличие в их работе возникает только на тех входных наборах, на которых =  = 1. При этом КЗ на поведение схемы не влияет (см. табл. 4.11). Все же остальные входные наборы, обнаруживающие неисправность  фиксируют также и замыкание . Поэтому

 = .                                      (4.30)

          На рис. 4.34 приведен пример схемы с КЗ без ОС.

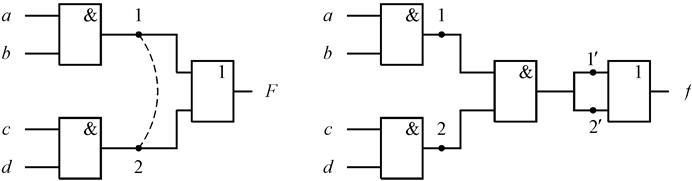
Рис.4.34.

 Схема реализует функцию . Для нее получаем: , , . Тогда

 =

 .

          Для неисправности  имеют место очевидные равенства

 =    и    = ,

где  и  – проверяющие функции неисправностей типа «константа 0» соответственно на линиях  и .

          С учетом этих равенств формулу (4.30) можно представить в виде

 = ,                                  (4.31)

или

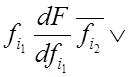
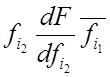 = .                          (4.32)

          Рассмотрим одиночное КЗ с ОС с четным числом инверсий. На рис. 4.35 приведен пример, иллюстрирующий данный вид замыкания.

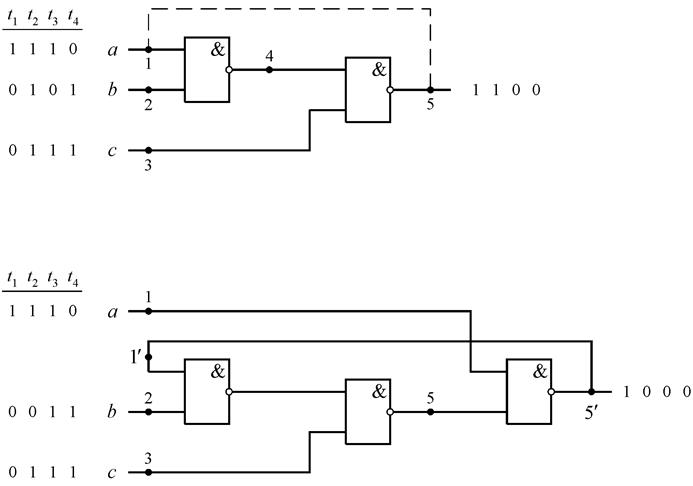
Рис.4.35.

Исходная схема (рис. 4.35,а) является комбинационной. Проверяющий тест схемы содержит 4 набора: {100, 111, 101, 011}. Наборы могут подаваться на вход схемы в любой последовательности. Предположим, что они подаются в тактах  в последовательности, приведенной на рисунке. Тогда на выходе схемы формируется последовательность 1100.

          Внесем в схему неисправность . Эквивалентная схема приведена на рис. 4.35,б. Если на ее вход подать указанные тестовые наборы в той же последовательности, что и на исходную схему, то на выходе схемы с КЗ формируется также последовательность 1100. Следовательно, тест на константные неисправности не обнаруживает КЗ.