Диагностирование логических схем на функциональных элементах, страница 26

          В отличие от детерминированного тестирования, когда обнаружение данной неисправности гарантированно, при случайном тестировании это происходит с некоторой вероятностью. Пусть испытуемая схема имеет п входов и пусть Е есть множество последовательностей из k входных векторов, которые могут быть приложены к схеме. Каждый входной вектор может быть одним из  векторов. Тогда Е содержит  элементов.

Предположим, что все входные векторы вырабатываются генератором случайных наборов с одинаковой вероятностью и что появление векторов в последовательности независимо друг от друга. Пусть  – множество последовательностей из Е, которые обнаруживают неисправность i. Мощность множества  равна .

Вероятность того, что один входной вектор не обнаруживает неисправность i равна . Вероятность того, что случайная входная последовательность длины  k  обнаруживает неисправность i равна:

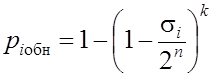.                                 (4.42)

Формула (4.42) позволяет получить ответ на следующий вопрос: дана схема и требуемая вероятность обнаружения данной неисправности; какова должна быть длина случайного теста.

Рассмотрим в качестве примера бесповторную двухуровневую схему (рис. 4.63).

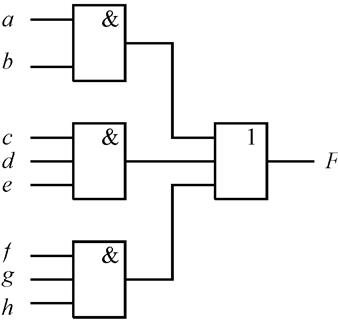
Рис.4.63.

 В табл. 4.14 приведена проверяющая функция для неисправности «константа 0» линии а. Эта функция содержит 50 двоичных наборов. Поэтому

.

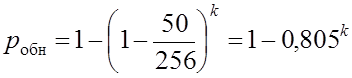      Т а б л и ц а   4.14

На рис. 4.64 показана зависимость вероятности обнаружения неисправности  от длины k случайного теста.

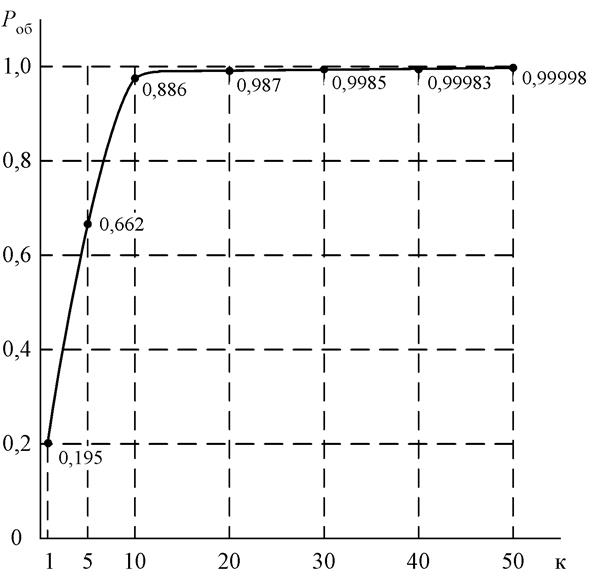
Рис.4.64.

 Например, чтобы обнаружить данную неисправность с вероятностью 0,99999 требуется подать на схему 53 случайных входных набора. В то же время, если подать на входы схемы детерминированный тест, неисправность  обнаруживается с вероятностью 1 на 6 наборах. Минимальный полный проверяющий тест схемы (рис. 4.63) содержит 6 наборов (см. табл. 4.15). Случайный          тест на 6 наборах обнаруживает неисправность  с вероятностью 0,728.

                                                                               Т а б л и ц а   4.15

          Бесповторная двухуровневая схема является наиболее легко контролируемой из логических структур. Этим объясняется такое явное преимущество детерминированного тестирования перед вероятностным в рассмотренном примере. В более сложных схемах такого значительного преимущества нет.