Диагностирование логических схем на функциональных элементах, страница 14

          Таблица путей заполняется по следующим правилам:

          1) на  пересечении -го  столбца  и -ой строки в клетке таблицы проставляется 0 или 1, если неисправность, соответствующая -му столбцу лежит на пути, соответствующему -ой строке;

          2) в клетке таблицы проставляется 1, если после неисправности по данному пути имеется четное число инверсий, и проставляется 0 в противном случае.

          Проекция неисправности на ЭНФ определятся по следующим правилам:

          1) неисправность, соответствующая -му столбцу, фиксирует в константы все буквы ЭНФ, в строках которых в столбце  проставлены 0 или 1;

          2) если на пересечении -го столбца и -ой строки в клетке таблицы проставлена 1, то вид фиксации (0 или 1) -ой буквы ЭНФ соответствует виду неисправности; если в указанной клетке проставлен 0, то вид фиксации буквы ЭНФ противоположен виду неисправности.

          Рассмотрим, например, неисправность под номером 7 (см. рис. 4.23). Она расположена на пути, соединяющим вход «b» с выходом схемы через элементы 5, 2, 1 (путь ), а также на пути, соединяющим вход «b» с выходом схемы через элементы 5, 4, 3, 1 (путь ). В пути  после неисправности 7 расположено четное число (нуль) инверсий. Поэтому в табл. 4.11 на пересечении столбца 7 и строки  проставлена 1. В связи с этим вид фиксации букв  в выражении (4.10) совпадает с видом неисправности 7 (константа 1). В пути  после неисправности 7 расположено нечетное число (одна) инверсий. Поэтому в табл. 4.11 на пересечении столбца 7 и строки  проставлен 0. Отсюда следует, что вид фиксации букв  в выражении (4.10) противоположен (константа 0) виду неисправности 7.

          В результате для неисправности 7 получаем следующую функцию неисправности:

.

          По функциям неисправности определяются проверяющий и диагностический тесты.

          Отметим, что существует полная аналогия между ЭНФ для схем на логических элементах и ЭНФ для контактных схем, описанных в главе 3 [1]. Буквы ЭНФ соответствуют контактам в контактных схемах или путям в функциональных схемах. Два пути называются совместимыми, если они вместе входят хотя бы в одну конъюнкцию ЭНФ. По этой причине для схем на логических элементах применимы модели, описанные в главе 3 – матрица совместимости и матрица отношений, а также основанные на этих моделях методы и алгоритмы.

4.3.5. Булево дифференцирование

          Удобным математическим аппаратом для анализа неисправных логических схем является аппарат булевых производных.

Определение 4.1. Булевой производной (булевой разностью) функции  относительно переменной  называется функция

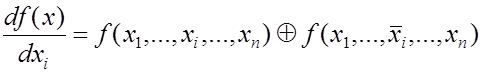 .         (4.11)

Значение булевой производной дает ответ на вопрос: изменяется ли значение функции  при инвертировании входной переменной . Поскольку ошибки на линиях схемы заключаются в ложном инвертировании сигналов на них, то аппарат булевых производных непосредственно применим к решению проблемы обнаружения ошибок и константных неисправностей в логических схемах.

При вычислении производных может быть три случая:

1) если , то ошибка в  будет вызывать ошибку на выходе , если  = 1;