Диагностирование логических схем на функциональных элементах, страница 15

2) если , то ошибка в  не вызывает ошибку на выходе , и, следовательно, функция  не зависит от переменной ;

3) если , то ошибка в  всегда будет вызывать ошибку на выходе  независимо от значения других входных переменных.

Рассмотрим схему на рис. 4.24.

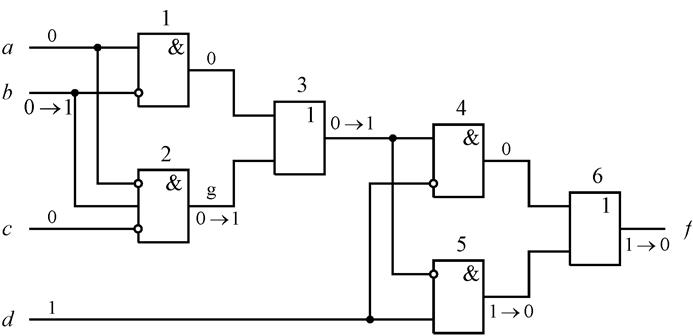
Рис.4.24.

 Она реализует функцию . Вычислим производную по переменной b.

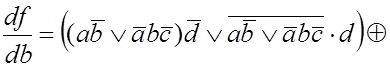
= {0, 1, 4,5, 8, 9, 10, 11, 12, 13, 14, 15) .                (4.12)

Таким образом, мы имеем первый случай. Результат (4.12) говорит о том, что ошибка на входе b приводит к ошибке на выходе f (транслируется на выход  f), если  a = 1 или с = 0, что выполняется на 12 входных наборах из 16. На каждом из этих наборов происходит активизация одного из четырех существенных путей от входа b до выхода  f.

          На рис. 4.24 показана активизация существенного пути b–2–3–5–6–f  на наборе 0001. Путь b–1–3–4–6–f активизируется, например, на наборе 1000, путь b–1–3–5–6–f – наборе 1001, путь b–2–3–4–6–f – на наборе 0000.

          Для иллюстрации третьего случая рассмотрим линейную схему (рис. 4.25).

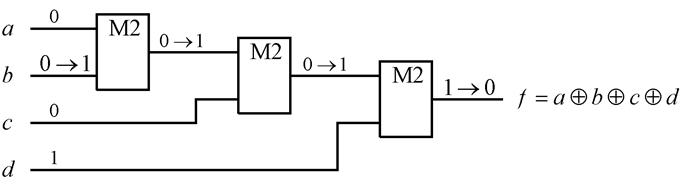
Рис.4.25.

 Для нее имеем:

.

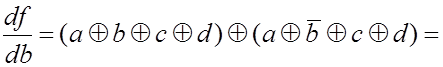
Этот результат отражает тот факт, что в линейной схеме ошибка на одном входе транслируется на выход независимо от значений сигналов на всех других входах.

          Для иллюстрации второго случая рассмотрим схему на рис. 4.26.

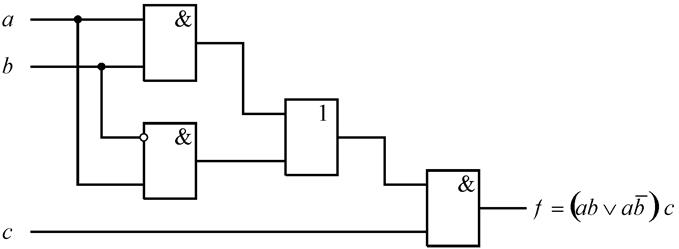
Рис.4.26.

 Вычислим

                         .

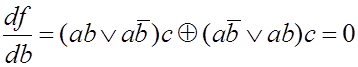Этот результат говорит о том, что функция  не зависит от переменной . В самом деле . Поэтому схема на рис. 4.26 является избыточной.

          Отметим   основные   свойства   операции   «сложение   по   модулю 2».

 ,                                      (4.13)

,                                         (4.14)

,                      (4.15)

,                                 (4.16)

,                                   (4.17)

,                               (4.18)

  или .                (4.19)

Учитывая данные равенства и формулу (4.11), можно вывести следующие свойства булевых производных:

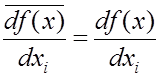,                                        (4.20)

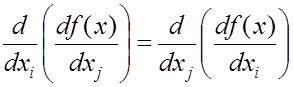,                            (4.21)

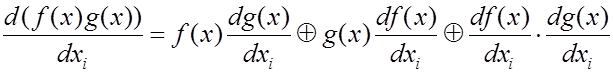,  (4.22)

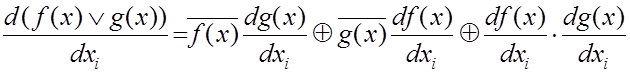,(4.23)

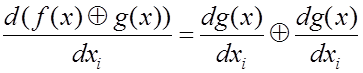.                        (4.24)

Формулы (4.20)–(4.24) могут быть использованы при вычислении булевых производных. Докажем еще одну формулу, удобную при вычислении .

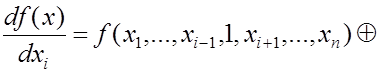
 .                         (4.25)

Она следует из соотношений:

.

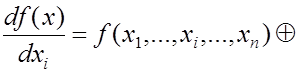
Используя формулу (4.25), вычислим производную  для схемы на рис. 4.24 (см. (4.12):

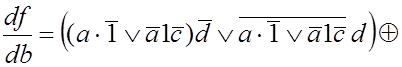
.           (4.26)

          Из сравнения процессов вычисления (4.12) и (4.26) видно, что использование формулы (4.25) дает существенное сокращение объемов вычислений. Из формулы (4.25) следует также, что булева производная не зависит от переменной , относительно которой она вычисляется.

          В простых случаях при небольшом числе переменных булева производная легко определяется с помощью карт Карно. Для этого составляется две карты для функций  и . Затем величины, записанные в соответствующих клетках карт, складываются по модулю 2. Результатом сложения является карта Карно, задающая производную . На рис. 4.27 показаны карты Карно при вычислении производной  для схемы на рис. 4.24 (см. также формулу (4.12)).

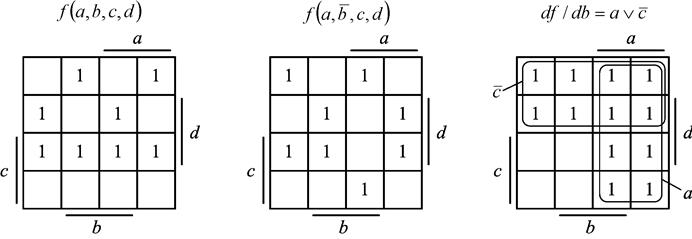
Рис.4.27.

          Рассмотрим теперь приложение булевых производных для обнаружения константных неисправностей на внутренних линиях логической схемы. Пусть надо найти проверяющую функцию неисправности на выходе элемента 2 (линии g) в схеме на рис. 4.24.  Введем   внутреннюю   переменную   g,  т.е.  представим  схему  (рис. 4.24) в виде схемы на рис. 4.28, в которой . Схема (рис. 4.28) реализует функцию .

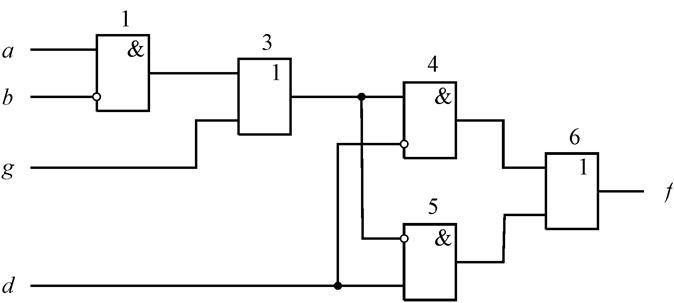
Рис.4.28.

          Как указывалось в разделе 4.3.2, для того, чтобы на данном входном наборе неисправность линии g была обнаружена необходимо и достаточно выполнение двух условий:

          1) неисправность проявляется на линии g, то есть инвертирует истинное значение сигнала на этой линии; если рассматривается неисправность «константа 0» («константа 1») то такой входной набор принадлежит множеству наборов, на которых на линии g реализуется функция  ;