который определяет входной набор 
= 0001, проверяющий неисправность 
. При этом активизируется D-путь 6–9–12–14.
D-алгоритм обеспечивает нахождение хотя бы одного проверяющего набора, если он существует. При рассмотрении всех возможных цепочек непустых пересечений вычисляются все проверяющие наборы и формируется проверяющая функция.
4.3.4. Метод эквивалентной нормальной формы
В данном методе для исходной схемы строится ей эквивалентная двухуровневая схема, которая описывается специальной формулой, получившей название «эквивалентная нормальная форма» (ЭНФ). Метод ЭНФ является аналогом метода путей и сечений для релейно-контактных схем, который описан в разделе 3.7. ЭНФ реализует ту же логическую функцию, что и исходная схема, а также отражает особенности ее внутренней структуры. Каждая неисправность исходной схемы при помощи определенных правил «проецируется» на ЭНФ, при этом находится множество неисправностей ЭНФ, которое эквивалентно рассматриваемой неисправности исходной схемы. Вычисление функции неисправности проводится не для исходной схемы, а для схемы, описываемой ЭНФ.
Рассмотрим метод построения ЭНФ [39] на примере схемы с разветвлением, приведенной на рис. 4.22.
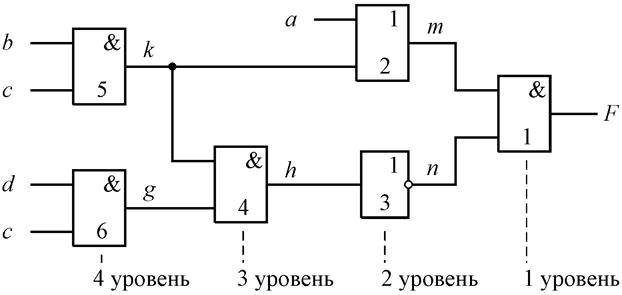
Рис.4.22.
Логические элементы обозначены цифрами и разделены по уровням. К уровню 1 относится выходной элемент схемы, к уровню 2 – элементы, выходы которых соединены со входами элемента 2-го уровня и т.д. Рассматриваемая схема содержит 6 элементов которые разделены на 4 уровня. Внутренние линии схемы обозначены буквами m, n, h, k, g.
ЭНФ находится путем серии последовательных подстановок, которая начинается с выходного элемента схемы. Выход элемента определяется через входы с указанием индекса, соответствующего этому элементу:
.
Далее в полученном выражении, переменные, отвечающие выходам элементов 2-го уровня, определяются через входы аналогичным образом:
.
Описанный процесс продолжается до тех пор, пока не будут рассмотрены элементы последнего уровня. В рассматриваемом случае осуществляются еще два этапа подстановок:
;
.
В полученном выражении раскрываются скобки при сохранении индексов элементов:
(4.9)
.
Выражение (4.9) является ЭНФ. Для нее характерны следующие особенности.
1. ЭНФ является логической суммой логических произведений, т.е. нормальной формой булевой функции.
2. Аргументами ЭНФ являются
буквы ЭНФ. Под буквой ЭНФ понимается переменная или ее отрицание с индексом
последовательности элементов определенного пути, связывающего эту переменную с
выходом схемы. Например, буква 
указывает путь от входа
«b» к выходу схемы через элементы 5, 2,
1. Число букв ЭНФ равно числу путей в схеме.
3. Число букв ЭНФ в общем случае больше числа входных переменных схемы, т.к. один и тот же вход схемы может быть связан с выходом несколькими путями. Например, вход с связан с выходом двумя путями: 5, 2, 1 и 5, 4, 3, 1.
4. ЭНФ может содержать
избыточные конъюнкции. В выражении (4.9) таковыми являются конъюнкции 
, 
и 
.
5. Если буква ЭНФ не имеет отрицания, то ей соответствует путь с четным числом инверсий; в противному случае – с нечетным числом инверсий.
Для упрощения записи ЭНФ последовательности элементов путей обозначаются цифрами:
2, 1 – 1; 5, 2, 1 – 2; 6, 4, 3, 1 – 3; 5, 4, 3, 1 – 4.
Тогда ЭНФ имеет вид
.
(4.10)
Для каждой неисправности исходной схемы находится ее проекция на ЭНФ в виде фиксации ее букв в константы 0 или 1. На рис. 4.23 представлено контрольное множество неисправностей рассматриваемой схемы.
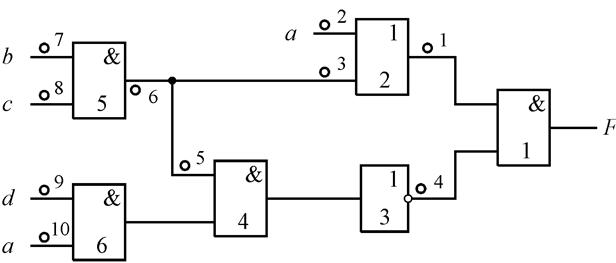
Рис.4.23.
Для определения проекций неисправностей строится таблица путей (табл. 4.11). Строки таблицы соответствуют буквам ЭНФ, а столбцы – неисправностям, входящим в контрольное множество.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.